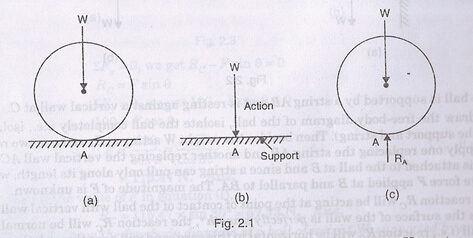
In the equilibrium of bodies, if the supports are removed and replaced by the supportive reactions then the free body diagram can be understood. Consider the figure below:
Here if the supportive surface is substituted with the reaction RA then that is an example of free body diagram.
- The point of application of the reaction RA will be the point of contact A, and from the law of equilibrium of two forces.
- We will concentrate upon that the reaction RA must vertical and equal to the weight W.
- Hence Fig.2.1 (c), in which the ball is completely isolated from its support and in which all forces acting on the ball are shown by vectors, is known a free-body diagram.
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Two dimensional force systems
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction
- Combined motion of translation and rotation
- Rectilinear motion in kinetics of particles
- Work and energy
- Linear momentum
- Force mass acceleration
- Simple stress introduction
- Normal strain
- Statically indeterminate system
- Introduction to thermodynamics
- Statement of zeroth law of thermodynamics with explanation
- Heat and work introduction
- First law of thermodynamics for a control mass closed system undergoing a cycle
- Open system and control volume
- Conversion of work into heat
- Introduction to carnot cycle
- Clausius inequality entropy and irreversibility introduction
- Ideal gas or perfect gas
- Introduction about air standard cycles
- Properties of pure substances introduction
- Vapour compression refrigeration cycle introduction
- Basic fluid mechanics and properties of fluids introduction
- Fluid statics introduction
- Manometers measurement pressure
- Fluid kinematics
- Bernoullis equation
- Basics and statics of particles introduction
Link of Next Mechanical Engineering Topics:-