The study of motion of any particle body without taking into account for the reason of such motion is known as kinematics. These motions are also known as forces due to which the particle bodies move. For an astronomical frame of reference or to see the working of primary inertial system, authenticity of information is provided by Newtonian mechanics.
In case of primary inertial reference frame, you will find it to be a figmental set of rectangular axes. These axes are reckoned to have no rotation or translation in space. When the word space arises in this concept, it is the term used for defining the geometric regions which are occupied by these bodies.
On taking account of such areas inside these rectangular axes, the positioning of these spaces is defined as per its area in it. Particle motion can be described in 3 axes formation.
- r,θ, z
- x, y, z
- R, θ, ϕ
These coordinates have different names that are generally used in kinematics.
- In case of r, θ, z; these are known as cylindrical coordinates.
- For x, y, z; these coordinates are known as Cartesian coordinates or rectangular coordinates.
- And finally for R, θ, ϕ; the given name of these coordinates is spherical coordinates.
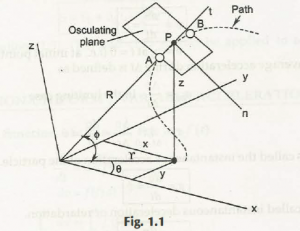
If calculation of particle bodies (P, A, B) are done in R, θ, ϕcoordinates, the motion of the body P can be related to the measurement along the tangent and normal, i.e., ‘t’ and ‘n.’These lines are to connected to the path which goes at point P. Lying in the local plane, which is also referred as the oscillating plane, ‘n’ is also connected to other points P, A, B.
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Two dimensional force systems
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
Links of Next Mechanical Engineering Topics:-
- Plane motion
- Rectilinear motion
- Analysis at constant acceleration uniform acceleration
- Analysis for non uniform variable acceleration
- Graphical representation x y plane graph
- Distance travelled in the second in constant acceleration
- Acceleration due to gravity