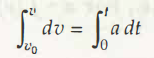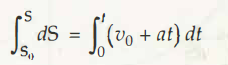To find out the final equation for constant acceleration, the following formulations are:
S = S0
t =0
v =v0
At point (1.2), the equation stands at dv = a dt
On integrating this equation, the calculation is,
An alternative to this calculation is v – v0 = at
v =v0 +at
Again on integrating on the seconds instance, the calculation stands to be,
The next step in this is,
v2 =v02 +2a (S –S0)
From the equation (1.1),
dS =v dt
dS = (v0+at) dt
so integration equation as per the above is,
S –S0 = v0 t +1/2 at2
S =S0 + v0 t +1/2 at2
P.S.
It is only in case of constant acceleration when equations (1.5), (1.6) and (1.7) are required to be applied.
Links of Previous Main Topic:-
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Plane motion
Links of Next Mechanical Engineering Topics:-
- Analysis for non uniform variable acceleration
- Graphical representation x y plane graph
- Distance travelled in the second in constant acceleration
- Acceleration due to gravity
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction
- Combined motion of translation and rotation
- Rectilinear motion in kinetics of particles