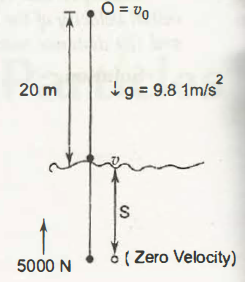
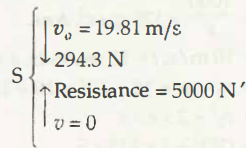Rectilinear motion is termed as the motion of particles of a rigid body such that each of them travels in a straight line and parallel to each other. Moreover, they travel the same distance as compare to one-another in the same direction.
Suppose the mass of one particle is m travels in x direction. The force applied in the particle is F in the same direction then,
According to Newton’s 2nd law of motion, distance travelled by the particle due to the action of external force is given by,
x = m. ax (This is a scalar product in x-direction)
Where,
ax = acceleration in x-direction
Considering the force in y-direction and z-direction,
y = 0
z = 0
Let us consider the particle has three components of acceleration such that ax, ay and az. In this case, force can be written as,
x = m. ax
y = m. ay
z = m. az
To calculate the value of acceleration, we determine,
= ax+ ay+ az
||= a = (ax2 + ay2 + az2)
Similarly,
Force, = x +y+ z
||=F = (Fx2 + Fy2 + Fz2)
The S.I. Unit of Force is
1 Newton (N) = 1 kg x 1 m/ s2
= 1 kgm/ s2
Example 5.1:
Suppose a body was in rest when an external force is acted on it. The force on the body produces 6 m/s2 of acceleration to give it some motion. If the mass of the object is 15 kg, then calculate the magnitude of force.
Solution:
Given Data:
Acceleration, a = 6 m/s2
Mass, m = 15 kg
We know that,
Force, F = m . a
= 15 . 6
= 90 N
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Two dimensional force systems
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction
- Combined motion of translation and rotation
Links of Next Mechanical Engineering Topics:-