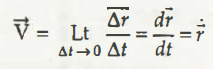Instead of moving in a straight line, if a particle body moves in a curved path (traverses), motion of that particle body will be known as curvilinear motion.
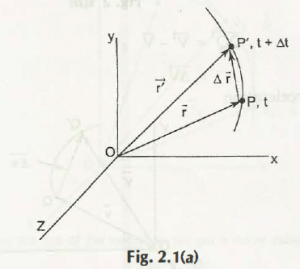
Suppose a graph is constructed with x, y, z coordinates. At a certain time ‘t,’let the position vector of a particle ‘P’ be ‘r.’ After sometime, the position vector ‘P’ moves to another position, making the new position ‘P’’. Its new time interval stands to be ‘M’. Time associated with the new position (P’) is t + ∆t, and its new position vector is ‘r’’.
After the graph is formed, you can see that in new time ‘M,’traversement of old point ‘P’ is to displacement ∆r.
When the limit of the particle is ∆t à 0, and its average velocity is seen to be,
V =
By combining the limit and velocity, you will get its instantaneous velocity, which is,
From the above equation, scalar magnitude of ∆r is found to be,
As you already know that average speed of the particle body is, instantaneous speed of it stands to be at,
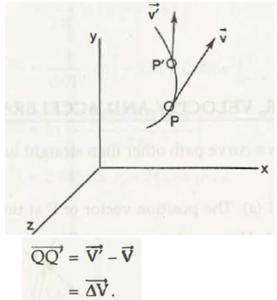
Now, let velocities at both points be derived with a certain name. Let velocity of P be V and velocity of P’ be V.’ When particle body changes their positions and velocities, time regarding that displacement will also get changed. In this case, the new time will be ‘t + ∆t’ from t.
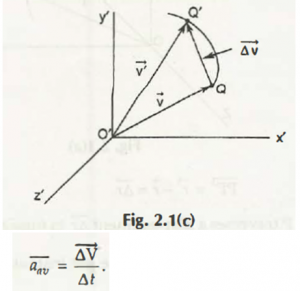
So from this change, a new equation comes out,
On further calculation, you will see its average calculation to be,
Instantaneous acceleration of that particle in limiting case,
The particle body P1 moves from P2 to P3, which cannot be stated as a path but a holograph. ‘A’ is found to be the tangent to that hodograph, which in this case is the acceleration of the motion. Also, changing ‘V’ is tangent to that particle path (hodograph). But when in consideration to the path of that particle, in ageneralized sense, ‘a’ cannot be termed as a tangent to that particle path.
Finally, when you add all the tips of velocity, the newly formed curve is called hodograph, which is mentioned previously.
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Two dimensional force systems
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
Links of Next Mechanical Engineering Topics:-
- Rectangular components of velocity and acceleration
- Projectile motion
- Tangential and normal components of acceleration
- Radial and transverse components
- Special case circular motion
- Relative motion