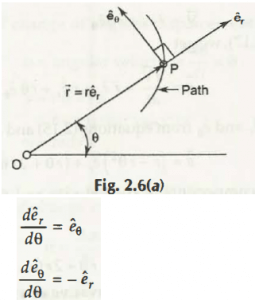
Suppose a certain graph is created in which a certain angle is formed whose planes are named as θ and r. It is via the provided plane information we will find out the dual components of a particle body.
Those dual components are acceleration and velocity of that particle which moves in both perpendicular and parallel lines. Both of those lines are depicted by 2 points D and P.
Now, from that drawn angle which describes the displacement of that particle body from one position to another position, that angle is depicted by θ.
From the formed figure, its equation stands to be,
After displacement, the new equation will be,
Negative sign in front of showcases the movement of that particle in its negative direction (r).
Links of Previous Main Topic:-
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Rectangular components of velocity and acceleration
Links of Next Mechanical Engineering Topics:-