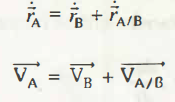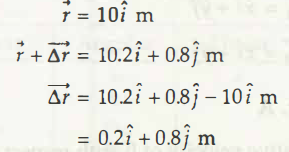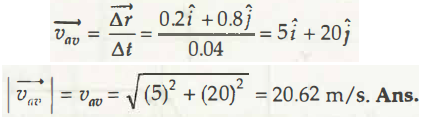Relative Motion of A with respect to B
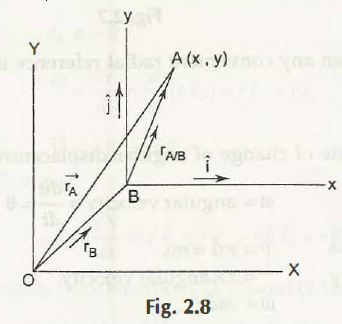
In a certain graph, whose fixed coordinates are X and Y,there are 2 particle bodies. Those particle bodies D and P have 2 vectors r and( r) ̇.
You will find the introduction of translating axes (x and y) here, as our objective of this graph creation is finding out the relative velocity of the first point D with respect to P. Moving to the next step, we will fix P as its moving origin.
Now, let those dual graphs be placed together with moving origins O and P. D is placed at a certain distance from P at a conclusive angle. As per the graph, you will easily understand the position vector of D with respect to P.
Differentiating the equation in accordance with respect to time, you will find the new equation to be,
( r) ̇D = ( r) ̇P + ( r) ̇ D/P
(VD) ⃗= (VP) ⃗+ V ⃗D/P
Equational problems and their solutions
Problem 1
Represented by 2 coordinates in a given graph where a particle body moves in 2 dimensional motions. The coordinates (x and y) have different values assigned to it. They are (y = 6 sin 2t) and(x = 2t2 -Bt + 40). In this case, time has been represented as ‘t’ and is in seconds. Calculate
a) Acceleration ‘a.’
b) Magnitudes of the velocity ‘V’ of that body, and
c) Angle A between time‘t’(given value 3sec) and velocity ‘V.’
Solution
a) Acceleration
v= √(v2x + v2y) = √((4)2+(11.522)2)
= 12.196 m/s
b) Magnitudes of the velocity ‘V’
From x axis,
x = 2t2 – 8t +40
vx=dx/dt = 4t – 8
vx at t = 3 seconds
= 4 x 3 – 8
=4 m/s
From y axis,
vy = dy/dt =12 cos 2t
vy at t =3 seconds
= 12 cos 2×3
= 12 cos 2x 3 x180°
= 11.522 m/s
c) To find the angle between time and velocity,
ax = dvx/dt
= 4 m /s2
Now from y axis,
ay = dvy/dt
= -24 sin 2t (reverse direction)
= -24 sin 2 x 3 x 180° / π
= 6.706 m/ s2
Problem 2
Position vector of a moving particle body in a graphical plane whose coordinates are x and y and at time ‘t’ have a certain value. Value of its position vector (r) is 10i ̂ m. when that particle changes its position, its new position vector is 10 2i ̂ + 0.8 j m. Calculate the magnitude of average velocity (vav) during that time interval when θ is the angle made that average velocity with x axis.
r ⃗=10i ⃗ m
r ⃗+ (∆r) ⃗= 10 2i ̂ + 0.8 j m
(∆r) ⃗= 10 2i ̂ + 0.8 j m-10i ̂ m
= 0.2i ̂ + 0.8 j m
At that interval time ∆t,
0.04 seconds – 0 seconds = 0.04 seconds
(vav) ⃗= (∆r) ⃗/(∆t) ⃗
= (0.2i ̂ + 0.8 j ̂)/0.04
= 5i ̂ +20 j ̂
⃒(vav) ⃗ ⃒= vav= √((5)2+(20)2)
= 20.62 m/s
So finally the calculation for finding that angle is,
tan θ = 20/5
=4
θ =tan-1 (4)
= 75.96°
Links of Previous Main Topic:-
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Rectangular components of velocity and acceleration
- Projectile motion
- Tangential and normal components of acceleration
- Radial and transverse components
- Special case circular motion
Links of Next Mechanical Engineering Topics:-