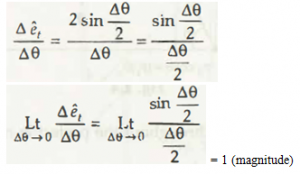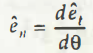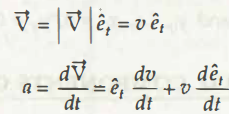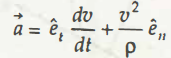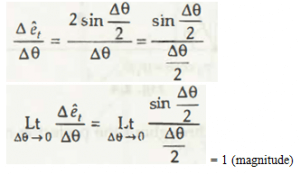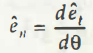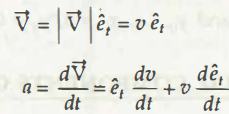Before going to tangential acceleration, you need to understand that in a generalized sense, acceleration is not tangent to the path of particle body. So the convenient resolution stands to be tangential acceleration into at angent and normal acceleration to the path on which the particle moves.
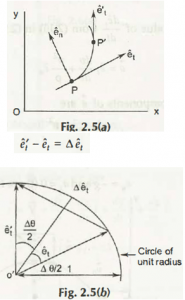
Suppose a graph is created whose unit vector tangent to the path is put as et
Initial point of a particle in this respect is considered to be P
Initial time taken by that particle to move in that path is supposed to be ‘t.’
When the particle displaces from its initial place P, its new position is seen to be P.’
New unit vector tangent to the path is put as et’
In this case, new time which was recorded after displacement of particle body is t+ ∆t
From the considered aspects stated above, you can see
Displacement of particle body from its initial position to its final position moves in a circular path which is known as circle of unit radius.
As per that movement, a new equation is formed.
Final answer after this calculation stands to be 1, which in this case is the magnitude of this tangential acceleration.
From the above calculation, you can see the unit vector which is
On the analysis of the next step, it is clearly seen that this new unit vector is directly perpendicular to the unit vector tangent of particle path et.
Now, when you consider to bring out the calculation for normal acceleration to the path on which a particle body moves, let us term that as en.
As per that,
From the above equation, we will proceed with the calculation including V, which is tangent to the path.
So the next step of that calculation will be,
As per all the above equations,
In the last case, p depicts the radius of curvature of that normal path on which that particle moves.
So finally, the calculation comes at,
On further substitution of values from to , the next equation which you will get is,
After establishing all these equations, you can see the scalar components of acceleration (a) are,
an= v2 p
According to this final equation, particle body moves in a certain path that has been named as the center of curvature.
Check all
Links of Previous Main Topic:-
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Rectangular components of velocity and acceleration
Links of Next Mechanical Engineering Topics:-