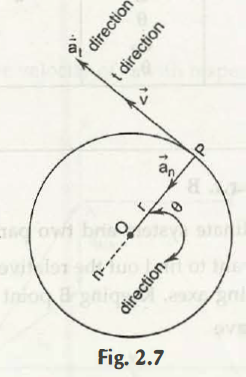
Suppose a particle is moving in a circular motion and we have to understand about its scalar components. In a generalized sense, those dual components are acceleration and velocity.
Let the 2 points of the straight line D and P be the half of the circular motion.
Let r, which is the radius of that circular path, be constant.
As per this information, calculations for both acceleration and velocity are:
v =r θ
an =v2/r = r θ 2 = v θ
at = dv/dt = v = rθ
Here, the measurement of ‘e’ is done from any side of convenient radial reference which then goes to DP.
Angular Velocity
The rate of change of a rotating particle body in an angular position is known as the angular velocity of that particle.
Angular velocity is represented as w
Equation for angular velocity is,
W = dθ/dt
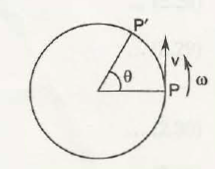
According to another figure of a particle moving in a circular motion, its linear velocity is represented as,
Linear velocity= r x angular velocity
The next equation stands at, v rθ = rw
Unit of angular velocity (w) = rad /s
Angular Acceleration
The rate of change of angular velocity is known as angular acceleration.
Its equational definition is,
a = dw/dt = d2θ/dt2 = θ = w
Equation for tangential equation is,
at = dv/dt = v = rθ
This calculation further goes to,
= r w = r dw/dt
= ra
In case of normal acceleration, its equation is,
v2/r = w2r2/r = w2r
Derivational equations for linear velocity are applicable for angular velocity.
If a certain instance is taken, equation for angular velocity is,
w = w0 +a tà
Equation for linear velocity is,
v = v0 +atà
Links of Previous Main Topic:-
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Rectangular components of velocity and acceleration
- Projectile motion
- Tangential and normal components of acceleration
- Radial and transverse components
- Special case circular motion
Links of Next Mechanical Engineering Topics:-