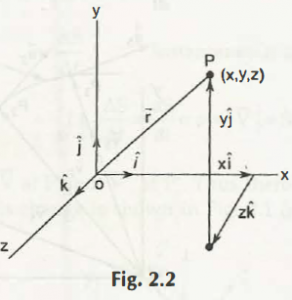
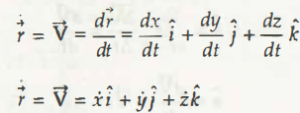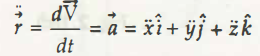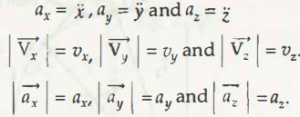Suppose there is a graph based on the x, y, z coordinates. From that graph, there is an equation, which is,
Referring from the same graph again, we get another equation,
On differentiating the above equation (2.2),
(Equation 2.3)
From the equation (2.3) you will get the scalar component of velocity which is,
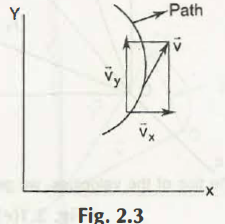
vx = x , vy = y and vz = z(Equation 2.4)
From the above equation, scalar components of accelerations,
ax= , ay = , az=
, ,
, ,
Links of Previous Main Topic:-
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Rectangular components of velocity and acceleration
Links of Next Mechanical Engineering Topics:-
- Projectile motion
- Tangential and normal components of acceleration
- Radial and transverse components
- Special case circular motion
- Relative motion
- Plane kinematics of rigid bodies introduction
- Combined motion of translation and rotation
- Rectilinear motion in kinetics of particles
- Work and energy
- Linear momentum