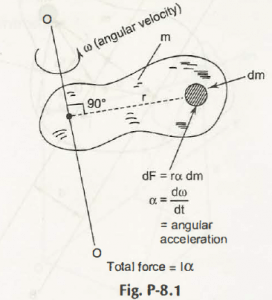
Let the mass moment of inertia of differential mass about 0 – 0 axis be dm as shown in Fig. P-8.1.
If it is perpendicular to plane of rotation of centre of mass, then it can be written as,
dI = r2 dm
or,
I = 2 dm
Where,
I = Mass Moment of Inertia
Keeping the mass density, p as constant, then we get-
dm = p dV
where,
dV = Element of Volume
Hence, from Fig. P-8.1,
I = 2p dV
= P2 dV
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Two dimensional force systems
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
Links of Next Mechanical Engineering Topics:-