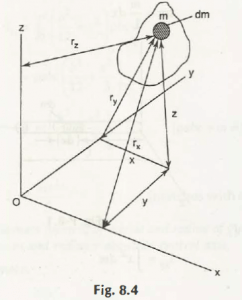
Consider the Fig. 8.4,
Let the mass moment of inertia about x- axis be Ixx
Mass moment of inertia about y- axis be Iyy
Mass moment of inertia about z- axis be Izz
So, it can be written as-
Ixx = x2 dm = 2 + z2) dm
Iyy = y2 dm = 2 + z2) dm
Izz = z2 dm = 2 + y2) dm
Suppose z is negligible as compare to x and y, then z = 0
Hence,
Ixx = 2 dm
= 2 x pt dA
= pt 2 dA
- Ix
Similarly,
Iyy = pt. Iy
Now,
Ixx + Iyy = pt (Ix + Iy)
= pt. Iz
Hence,
Ixx + Iyy = Izz
Considering the above Equations, 8.8 is for thin flat plate and whenever we calculate differential mass dm for element of thickness dz
Thus, it can be modified as-
dIxx + dIyy = dIzz
Example 8.1:
Suppose a slender rod of length L, mass m which is perpendicular to the axis where x-axis is passes through it as shown in Fig. P-8.1.
Find its mass moment of inertia
Solution:
Take, dm = m/ L dx
Thus,
The mass moment of inertia about y-axis can be calculated as,
Iyy = 2 dm
= m/ L x 1/ 3 x L3
= mL2/ 3
Links of Previous Main Topic:-
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Radius of gyration in mass moments of inertia second moment of mass
- Transfer of axis
- Mass moment of inertia about x axis y axis z axis
Links of Next Mechanical Engineering Topics:-