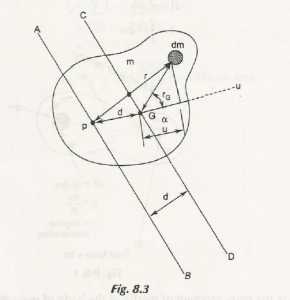
Considering the Fig. 8.3,
Suppose AB and CD are two parallel lines. AB passes through any point P of a rigid body and CD passes through its centre of mass, G.
From trigonometry, we get the calculation as-
r2G + d2 +r2/ 2rG d
= r2G + d2 +r2/ 2rG d
2r2G+ d = r2G + d2 – r2
r2 = r2G + d2 + 2rGd
Now,
I = 2dm
= 2G + d2 + 2rGd } dm
=2Gdm + d22Gdm
= IG + d2m + 2d dm
= IG + md2 + 0 (Since, dm = 0)
Hence,
I = IG + md2
Similarly, we can calculate,
K2 = K2G + d2
Where,
KG is the Radius of Gyration
Links of Previous Main Topic:-
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Radius of gyration in mass moments of inertia second moment of mass
Links of Next Mechanical Engineering Topics:-