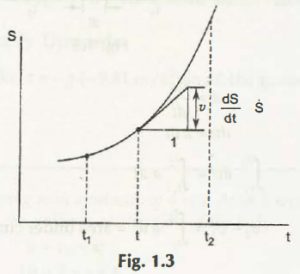
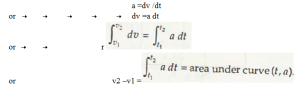1.The first graph from the figure 1.3 and equation 1.6.1, it shows that a particle body moves in a rectilinear motion whose variational position is from ‘S’ to ‘t.’ The given time between the variations is from ‘t1’ to ‘t2’.
According to the formation of the graph, slope of it is calculated to be = u
- As per another graph in equation 1.6.2, which is a (v, t) graph,
Variation of path from v to t in a rectilinear motion within the given time ‘t1’ to ‘t2’, calculation of slope stands to be at = a
Elemental area of slope is v dt,
Which finally goes to be dS = v dt
Integration formula of it is,
In this case, v dt is depicted as area under (u, t) curve
-
- As per third graph in equation 1.6.3, which is a (a, t) graph,
Here, a dt is calculated as area under thecurve.
Links of Previous Main Topic:-
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Plane motion
Links of Next Mechanical Engineering Topics:-