Rectilinear motionis the term used for depicting a straight line, or to be specifically speaking, the path in which the particles are in motion.
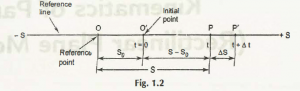
In a straight line, ‘-S’ is used for depicting the initial point of that line whereas ‘S’ is used for showing the end of that line. A certain particle ‘r’ is seen moving along that straight line. In between the reference line with points ‘-S’ and ‘S,’there are 4 more points.
Among those 4 points, O is taken as the initial position S = S0 and P at t = 0. In this case, P is the position of a particle at time ‘t.’
At a certain distance from the point P, there is another point P’.
For that position, its calculated time =t+ ∆t.
Displacement in ‘m’ for aunit time =∆S /∆t.
Displacement in time is ∆t =∆S.
In case of ∆t à 0, which is a limiting case, velocity is calculated as V = Lt
Average velocity is taken to be as ∆S /∆t = Vav
Equation for instantaneous velocity, which is also depicted as V is ∆S /∆t= dS /dt.
This again on equating comes to be as v = dS/dt =S.
The velocity when calculated at initial point O stands to be V = Vo. Time in this respect is 0.
After designating all the formulations, the definition of average acceleration which takes place during the time depicted by ∆t is aav =∆v / ∆t (equational term). In here, ‘a’ is defined as instantaneous acceleration of that particle.
In limiting case, the equation for it is a = dv /dt =v.
When considering for‘-a’, it is equivalent to retardation or instantaneous deceleration. So, on this context, a d2S / dt = S
From the first equation we have (dt = dS /v)
And from the second equation, we have (dt = dv / a)
Therefore, calculating with both equations, the final answers stands to be,
(dt = dS /v = dv /a)
And (v dv =a dS)
Links of Previous Main Topic:-
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Plane motion
Links of Next Mechanical Engineering Topics:-
- Analysis at constant acceleration uniform acceleration
- Analysis for non uniform variable acceleration
- Graphical representation x y plane graph
- Distance travelled in the second in constant acceleration
- Acceleration due to gravity
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction
- Combined motion of translation and rotation
- Rectilinear motion in kinetics of particles