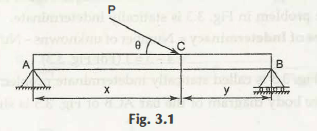
In the given diagram ACB we just need to draw a free body. Here, x, y and P and the angle are known. In addition, the weight of the bar is considered as negligible and thus it is neglected.
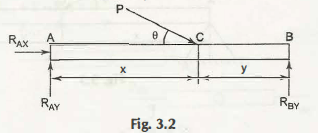
If we make it a perfect diagram with free body, then it would be just like the following
What are the unknown numbers here? These are 3 numbers as RBy, RAX and RAy.
Now, the number of equations available are –
Σ M = 0
Σ fy = 0
Σ fx = 0
These are also aviable in 3.
It means the number of unknowns = Number of equations available.
These kind of problems are known as statically determinate problems. The exact problem is prvded in the first figure.
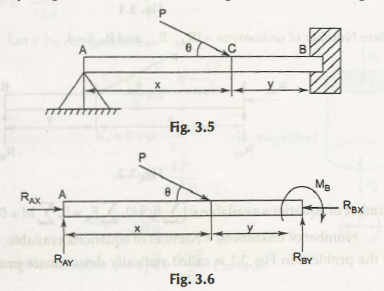
To make the solution ins a proper way the following two diagrams are important to understand –
Here the number of known quantities is 4 as P, x, θ and y. The weight is neglected.
Now, the number of unknowns are RAx, RBy, RAy‘, RBx = There are 4 unknowns for this
The number of equations = 3
These 3 equations are – Σ fx = 0, Σ fy = 0 and Σ M = 0
Here, if you compare
Number of unknowns > number of equation availability
This kind of problem is known as statically indeterminate.
Now, Degree of Indeterminacy
= Number of unknowns – Number of equations available
= 4 – 3
= 1
It indicates that Degree of Indeterminacy is 1.
It can also be said as degree one of the statically indeterminate problem.
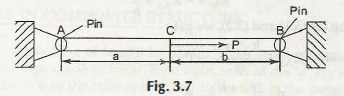
The following diagram shows some other problem as
Statics equations are available = 3
Number of unknowns = 5 = RBx, RBy, RAx, RAy‘and MB.
Now the degree of indeterminacy can easily be evaluated as
Degree of indeterminacy = 5-3 = 2
Solutions related to the problems
If this figure is the problem, that you need to solve.
Now, go through carefully and you will get that Unknown numbers = 4
Avilable equations = 3
Degree of determinacy = 4-3 =1
By neglecting the bar’s weight the RAy addition of vertical reactions will be zero.
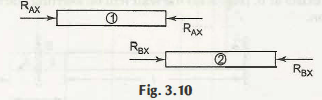
Now, consider the give case
Σ fx = 0 =>
RAX + P – RBX = 0
RAX – RBX = – P
Here it is important to find out another equation.
Elastic deformation for bar ACB
Two supports = Perfectly rigid (Assumed)
The total deformation for the total length (a + b) = zero.
δ1 = -RAx x a / AE
δ2 = – RBx x b / AE
δ1 + δ2 = 0
RAx x a + RBx x b = 0
RBx = – RAx x a /b
Now, after getting through both equations
RAx x a / b = p
RAx ( a +b / b) = p
RAx = pb / a+b
RBx x a /b = – pa / a +b
It means the exact direction of R ax will be completely opposite to the direction of P.
After understanding this you can easily solve the different problems.
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Two dimensional force systems
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction
- Combined motion of translation and rotation
- Rectilinear motion in kinetics of particles
- Work and energy
- Linear momentum
- Force mass acceleration
- Simple stress introduction
- Normal strain
Links of Next Mechanical Engineering Topics:-