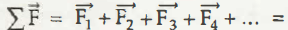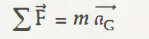According to the newton’s second Law of motion F = ma
This also expresses that if forces are applied and act on a rigid body, then
Angular momentum of its centre of the gravity = Acceleration of G or the center of the body.
It means if the different forces are applied on the rigid body then their sum will be the resultant of all external forces. It means
till the end magnitude of the force in your equation
and thus Let
Resultant of all forces those act on a body.
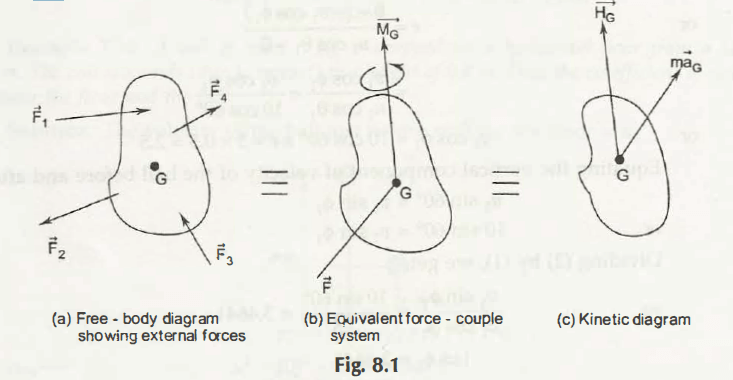
Now, what are the conditions of forces those act on a rigid body? To get its proper answer look at the following figures.
In the figure (a), The different forces F1, F2, F3 and F4 act and the different forces are some external forces. In the figure (b) Equivalent force shows the couple system and in the last figure you can get that kinetic forces act. Now, the G is the center of gravity. HG represents the angular momentum of the center of the gravity.
HG = Angular momentum of the body having G is the centre of Gravity = Acceleration of the body with the mass centre G
According to the second law of Newton,
F = ma
Here,
Where, m is the body mass.
An important concept here is the summation of moments about the mass centre = time rate of change of the angular momentum
Now, it is clear that the working of the external forces can be expressed by the next figure as couple system G. In addition, by using equation from the figure (a) and using equation from the figure (b), the Kinetics digram figure c is derived.
Now, it is clear that how force mass and acceleration are related to each other and how gravity plays an important role in finding out the relation.
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Two dimensional force systems
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction
- Combined motion of translation and rotation
- Rectilinear motion in kinetics of particles
- Work and energy
- Linear momentum
Links of Next Mechanical Engineering Topics:-