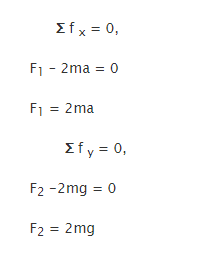The equation of motion of a rigid body can easily be derived through D’ Alembert’s Principle and it is used to study static equilibrium of that body. Now, to have a proper explanation of this, a diagram can easily clear the things.
So, according to the Newton’s second law of motion
Go through this figure below –
Here, the fixed coordinate is (X,Y) in where a particle of mass m is placed. Now, the moving co-ordinate (x,y) has introduced a single particle m and thus it can be shown as –
The forces act on this particle are
Here the term – ma, which is an inertia of force, and this can be in equilibrium or rest. At he moment when all forces acting on mass m, then its resultant value will be zero.
Now, what type of equilibrium is there? It is none other than the dynamic equilibrium. Now, the co-ordinates that move can be written as
Now, this is the D’Alembert’s principle which finds out the static problem through apparent or the virtual transformation of its dynamic problems. It directly states that the summation of moments at any particular point P will give the resultant as zero. The negative sign shows the opposite direction of the real forces.
According to this principle “ Similar to the equations of static equilibrium, equation of dynamic equilibrium can also be established by introducing the inertia force in the direction opposite to the acceleration in addition to the real forces.”
All the factors as Static Equilibrium, Dynamic equilibrium and Generelized inertia force are important factors.
Links of Previous Main Topic:-
- Combined motion of translation and rotation
- Rectilinear motion in kinetics of particles
- Work and energy
- Linear momentum
- Force mass acceleration
- X y plane motion equations
- Translation in plane kinetics of rigid bodies
- Kinetic energy in plane kinetics of rigid bodies
Links of Next Mechanical Engineering Topics:-