The kinetic energy is the energy present in a body when it is in motion. The motion of the body can have due to vibration, rotation or translation. The motion in translation means from one point to the other or from a location to any other location. The Kinetic energy is directly proportional to the square of the speed of the particle.
The finding out the Kinetic energy depends on two different terms as mass m and speed v. One more important thing to know about this is its proper quantity, and it is not a vector quantity, but it is a scalar quantity. Now, dm is the mass of the particle in a rigid body that changes its position.
dT i = 1/2 x dm I x vi2
= 1/2 dm i x v2
Here, vi = v
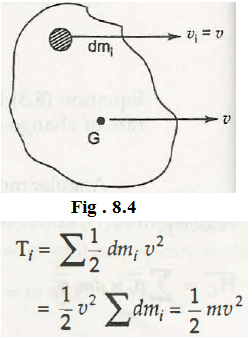
Now, the equation for the whole can easily be concluded by taking the sum of the small part with the mass dm. G is the center of the mass.
The KE of translation can be derived with the following way –
From the above equation it is clear that how the total mass m with speed v make the energy perfect. Thus, KE of an object can easily be derived through the formula KE = ½ mv2.
Links of Previous Main Topic:-
- Combined motion of translation and rotation
- Rectilinear motion in kinetics of particles
- Work and energy
- Linear momentum
- Force mass acceleration
- X y plane motion equations
- Translation in plane kinetics of rigid bodies
- Kinetic energy in plane kinetics of rigid bodies
Links of Next Mechanical Engineering Topics:-