Equilibrium of any stationary body occurs when external forces, either concurrent or parallel forces are to act upon a rigid body but no movement or rotation is resulted as its reaction. In that position the body is said to be in equilibrium. In this chapter you are going to find:
- Conditions of equilibrium for the external forces both concurrent and parallel separately.
- Moment of force on a point and in an axis.
- Varignon’s theorem.
- Free body diagram.
- Vectorial representation of moments and couples.
- Many types of support reactions.
- And what is the determination of reaction will be explained.
In the next portion, equations of equilibrium will be focused, such as:
-
- Equations of equilibrium: When studying equilibrium of rigid body, then there will be mentions on coplanar forces or as it is explained as concurrent and parallel forces. In the equilibrium state of the stationary body all mathematical outcome of external forces will become zero with the moments about the point and axis. The equation will be written as F = 0 and M = 0. The first equation is known as force law of equilibrium and the second one is known as the moment law of equilibrium. The forces are generally resolved into horizontal and vertical components. Hence equation (first) is written as Fx = 0 Fy= 0 whereFx= Algebraic sum of all horizontal components andFy= Algebraic sum of all vertical components.
- Equation for non-concurrent forces: This equilibrium occurs when all other forces and moments reach a mathematical result of zero. The equation is Fx = 0, Fy = 0 and M = 0.
- Equation for Concurrent forces: In this equilibrium all lines of actions are found in one point and so ultimately making moments of those forces also zero. Here M = 0 becomes unnecessary and the important equations remain as in Fx= 0 and Fy= 0.
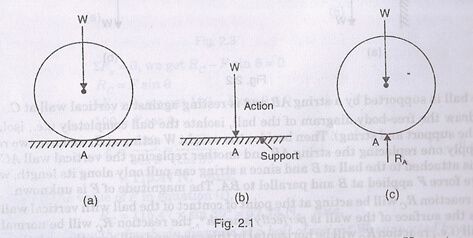
- Action and reaction: In the third law of Newton, all actions have an equal amount of opposite reaction. This is an equal power of opposite features. In the figure below there are two balls placed horizontally. They can move freely horizontally but not vertically down. The ball will place an action which wants to move downward. The support will place an equal amount of opposite force to stop that ball to go downward than is calld reaction.
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Two dimensional force systems
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction
- Combined motion of translation and rotation
- Rectilinear motion in kinetics of particles
- Work and energy
- Linear momentum
- Force mass acceleration
- Simple stress introduction
- Normal strain
- Statically indeterminate system
- Introduction to thermodynamics
- Statement of zeroth law of thermodynamics with explanation
- Heat and work introduction
- First law of thermodynamics for a control mass closed system undergoing a cycle
- Open system and control volume
- Conversion of work into heat
- Introduction to carnot cycle
- Clausius inequality entropy and irreversibility introduction
- Ideal gas or perfect gas
- Introduction about air standard cycles
- Properties of pure substances introduction
- Vapour compression refrigeration cycle introduction
- Basic fluid mechanics and properties of fluids introduction
- Fluid statics introduction
- Manometers measurement pressure
- Fluid kinematics
- Bernoullis equation
- Basics and statics of particles introduction
Link of Next Mechanical Engineering Topics:-