Thevenin’s theorem states, “the network where RL is connected diagonally with two different terminals also containing the sources of resistors and electromotive forces can be interchanged by series resistor Rth and also by solitary source of electromotive force respectively. Under this electromotive force e.m.f:
- Eth will be equivalent to possible variance in the network terminals while removing R which is the resistor from the network.
- Rth which is the resistance number of the series resistors will be equivalent to the network resistance while removing the resistance R from the network.
Hence I= E /(RL + R th) (cannot be changed)
Let’s explain the stated theorem in detail:
Explanation.
We have to find the current value concluded with the load resistance RL as mentioned in the figure 66 (a). We will monitor the following steps:
- We need to redraw the circuit after removing RL after the terminals A and B of the circuit. Please note that the terminals will be an open circuited here.
- We will calculate Voc = Eth that is open circuit voltage when RL is removed appearing across A and B which are the open. Please note that Eth is the Thevenin’s voltage here.
- We will find Rth which is the Thevenin’s resistance across the terminals of A and B by short circuiting the battery.
R th = R1 x R2 / R1 + R2 (cannot be changed)
- We will get the value of current through by reconnecting RL back to the position across the terminals A and B as:
I = E th / ( R th + RL) (cannot be changed)
After discussing the detailed explanation and statement of theorem, let’s understand the same though examples:
Example 1.
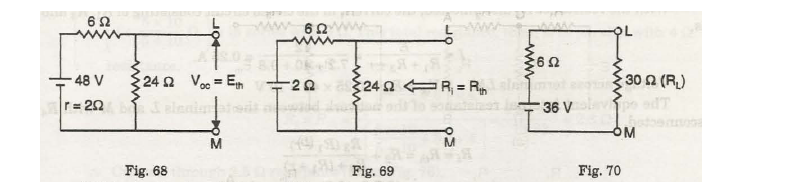
Use Thevenin’s theorem and calculate the following value by considering figure. 67
- When observed from terminals Land M, calculate the value of m.f. of the network.
- When observed into from terminals L and M, calculate the value of equivalent resistance of the network
- Calculate current value in the load resistance RL of 30 n.
Solution
Equivalent value of e.m.f. of the network:
Refer Fig. 67.
Before connecting load resistance (RL), the value of the network current is
= 48 / 24 + 6 + 2 = 1.5 A (cannot be changed)
Voltage value diagonally with terminals LM,
V oc = Eth = 24 x 1.5 = 38 V. (cannot be changed)
The network will have the value of electromotive force as 38 V till the terminals L and M are connected. (Answer)
(ii) Correspondent value of resistance in the network :
To calculate the equivalent resistant, assume that 48 V of battery is removed. Please note that the internal resistance is still present under two parallel path between the terminal L and M.
We can look at the resistance from the terminals L and M as:
R1 = R th = 24 x (6 x2) / 24 + (6 + 2) = 6 Q (cannot be changed)
(iii) Current value in RL,I:
As per Fig. 70.
I = E th / R th + RL = 36 / 6 + 30 = 1 A (cannot be changed)
Example 2
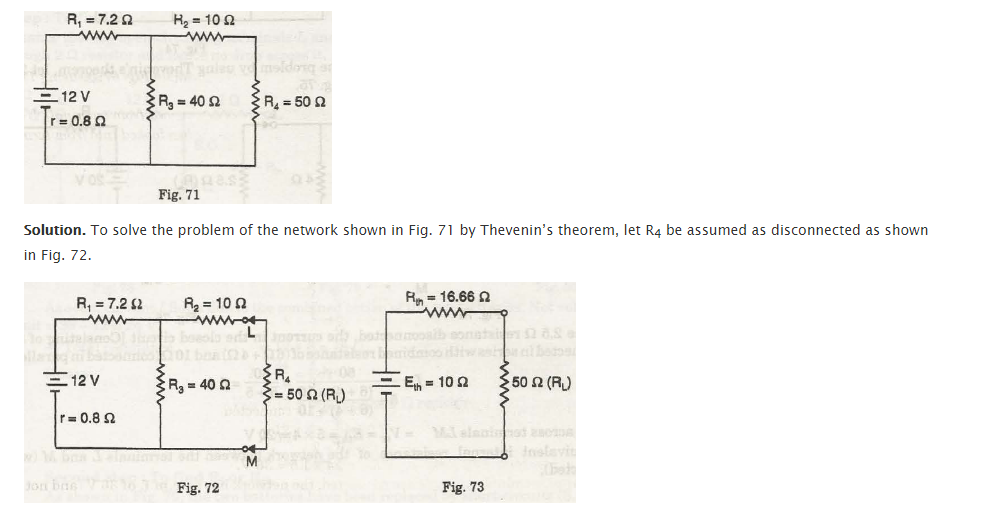
Use Thevenins’ theorem to calculate the current value with 50 Ohms value of resistance of the circuit as shows in figure 71
Solution
Let’s assume R4 as the disconnected resistance as briefed in the figure 72 to calculate the value by Thevenin’s theorem
The current value in the circuit which is closed and consists of Rh R3 and
r is,
I = E / R1 + R3 + R = 12 / 7.2 + 40 +0.8 = 0.25 A (With the resistance R4 disconnected)
(cannot be changed)
The Voltage value diagonally to the terminals LM
= V oc = Eth = 0.25 x 40 = 10 V
(cannot be changed)
The corresponding value of the internal resistance in the network with R4disconnected,around the stations L and M will be:
R i = R th = R2 =R3 (R1 + R / R1 + r)
= 10 + 40 (7.2 + 0.8) / 40 + 7.2 + 0.8 = 10 + 40 x 8 / 48 = 16.66 Q
The value of the Current through 50 Q (RL) resistances
I = E th / R th + RL = 10 / 16.66 + 50 = 0.15 A
(cannot be changed)
Link of Previous Main Topic:-
- Current Electricity Basic Concepts
- Definitions of Important Tenns Relating Network
- Limitations of Ohms Law
- Kirchhoffs Laws
- Applications of Kirchhoffs Law
- Source Conversion
Links of Next Electrical Engineering Topics:-