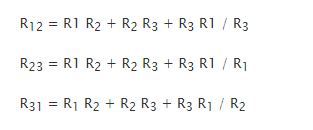One can find it difficult to solve the numerous simultaneous equations with the help of Kirchoff’s law when the network has huge number of divisions. But if you replace the corresponding systems of stars with delta meshes (the same is applicable in vice- versa format), it will be an easier calculation to solve as compared to the complex equations and calculations.
Let’s consider both the circuits as shows in Figs.- 102 and 103. If resistance is measured between two any of the terminals are same in both the cases, it will be equal.
From the equation above, we can say that the calculated resistance of the star of each arm is assumed by the merchandise of the two delta resistances sides meeting at the end is divided by the addition of delta resistances of three.
We can also obtain the start to delta conversion with the help of (24) to (26), eqns which are as follows:
in electronics,
Circuits of star and delta are generally referred to as ‘t and 1t circuits individually.
Let’s consider few examples:
Example 1
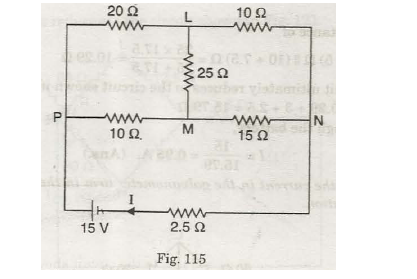
Using the concept of delta/star transformation, find the value of the current I which is supplied through the battery for Fig. 115,
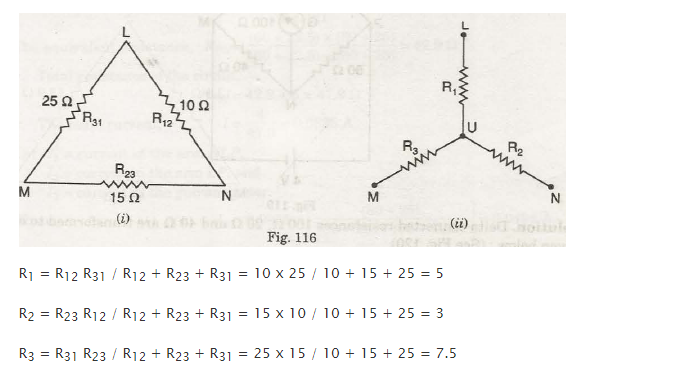
Solution. Resistances value connected in Delta 25 n, 10 n and 15 Q are converted to equivalent star as given below : (See Fig. 116)
The given circuit is moderated to circuit as shown in Fig. 117.
The equivalent resistance of
Hence the given circuit ultimately diminishes to the circuit shown in Fig. 118.
Therefore, the value of the current across the battery,
Example 2
By using Δ-Y transformations, find the resistance at the A-B terminals in the electric route of Fig. 126
Solution
By converting CEF to the star connection, we will get
Example 3
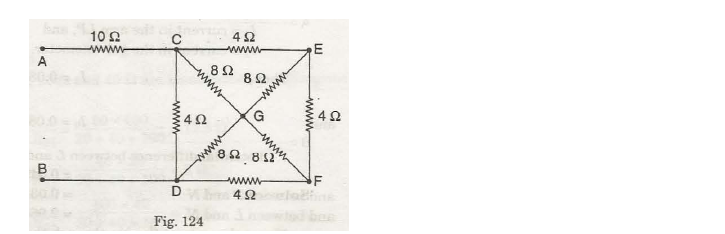
Refer to figure 124, and find the resistance between the terminal AB using delta/star conversion method
Solution
When applying conversion of delta-star to CGD and EGF in the figure Fig. 124, it results into Fig. 125 (i).
We will notice the reduction in the circuit to the equivalent by further simplification as illustrated in figures 125 (ii) and 125 (iii ).
Now converting CHJ to similar star as in B Fig.125 (iv).
Using the combination of series-parallel, we have
Link of Previous Main Topic:-
- Current Electricity Basic Concepts
- Definitions of Important Tenns Relating Network
- Limitations of Ohms Law
- Kirchhoffs Laws
- Applications of Kirchhoffs Law
- Source Conversion
Links of Next Electrical Engineering Topics:-
