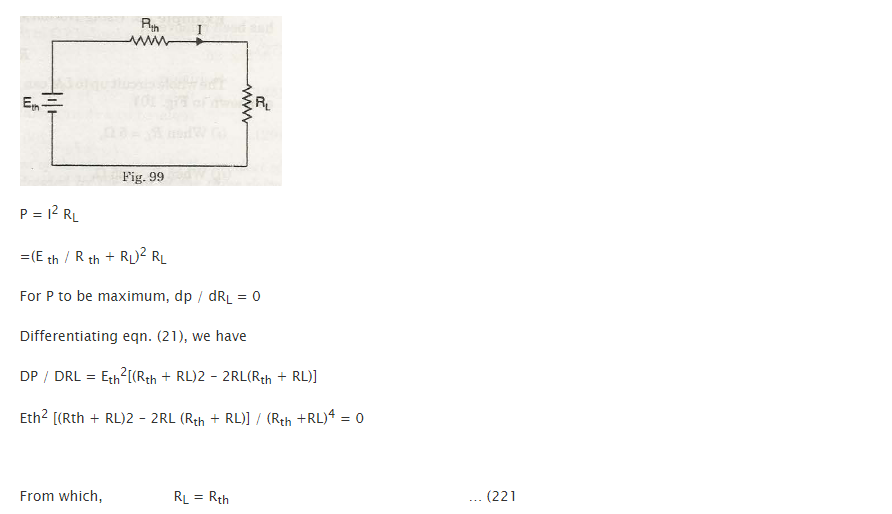
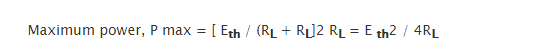The maximum power transfer theorem states, “When the resistance of the load and the network output resistance is equal as seen in the stations of the load, it can help in attain maximum power output”
This theorem is best suited to analyze the communication networks.
As we know through Thevenin’s theorem, that a conversion is possible of any network into voltage of single source. The maximum power transfer theorem thus aims in maximizing the power degenerate in RL at Rth 1 finding RL.
Since the value of voltage across these conditions is half of the open circuit voltage, it is not worth the calculation at the terminal L and M.
‘Load matching’ refers to the process to maximize power transfer by adjusting the resistance load which is referred in the mentioned cases:
- Where battery is coordinated to the starter motor: Motor Cars/vehicles
- Where television instruments are matched with the respective TV receiver: TV leads and lines of telephone
Let’s apply the theorem in an example now:
Example
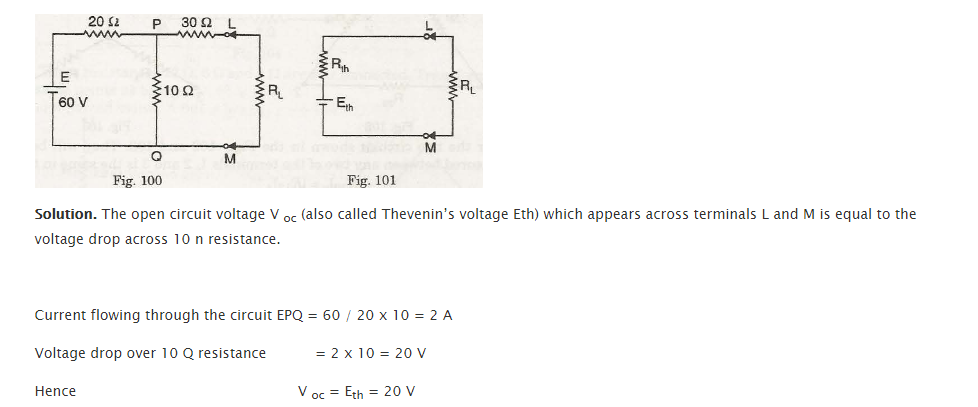
If the current value is taken as 5 and 25 Q, find the current value through RL as shows in figure 100.
When the power is dissipated in RL is maximum, calculate the value of RL
Also calculate its Power value and
Solution
The value of the voltage V oc with open circuit (also called Thevenin’s voltage Eth) is similar to the value of the voltage drop diagonally 10 n resistance which appears across terminals L and M
The circuit resistance when the battery has been removed can be looked as into.
From points L and M, the network
We can replace the circuit till LM by electromotive force of single source and resistance.
- When RL = 5 Q,
- When RL = 25 Q,
We can say that the value of power drawn with RL will maximize when
RL = R; or when
RL = 36.67 Q,
as per the statement of maximum power theorem.
Therefore, The value of Maximum power drawn by
Link of Previous Main Topic:-
- Current Electricity Basic Concepts
- Definitions of Important Tenns Relating Network
- Limitations of Ohms Law
- Kirchhoffs Laws
- Applications of Kirchhoffs Law
- Source Conversion
Links of Next Electrical Engineering Topics:-