Norton’s theorem states, “ The voltage which is independent and sources of current carried on two liners network terminal can be replaced with equal IN current and resistance RN which is parallel to IN, with:
- IN is termed as the current which is short circuit in the network terminals,
- RN is termed as the similar resistance value of network in the terminal.
But it is considered when the voltage sources are circuit short and every current source is also open circuited.
As compared to Thevenin’s theorem, this theorem helps in resolving the network parallel resistance with constant current source while Thevenin’s theorem resolved the same with series resistance and not parallel.
Explanation:
While considering Norton’s theorem, please follow the succeeding points:
- At the network terminals, first calculate IN (short circuit current)
- Now the network will be redrawn by replacing:
- Voltage source by internal resistance of short circuit in resistance in series
- Source of current by circuit which is open and also parallel with the internal resistance
- After procedure of redrawing is complete, now calculate RN (resistance) from the terminals of the network
Please note that RN which is the value of resistance is equivalent to the Thevenin’s equivalent circuit.
Let’s understand the concept more clearly with the help of examples:
Example1
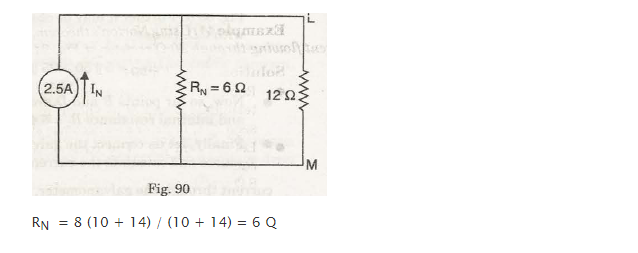
Calculate current value in 12 Q circuit resistance, by using Norton’s theorem as shown in Fig. 89.
Solution
– With terminals L and M as short circuited and 12 Q resistance removed, short-circuit value of current is
In=20/8 = 2.5 Ans.
– the value of the resistance in the network which can be seen with terminals L and M with the 20 V of battery which is replaced by a short circuit is
We can find the Norton’s equivalent circuit in Fig. 90.
The value of the current concluded with 12 Q resistances is
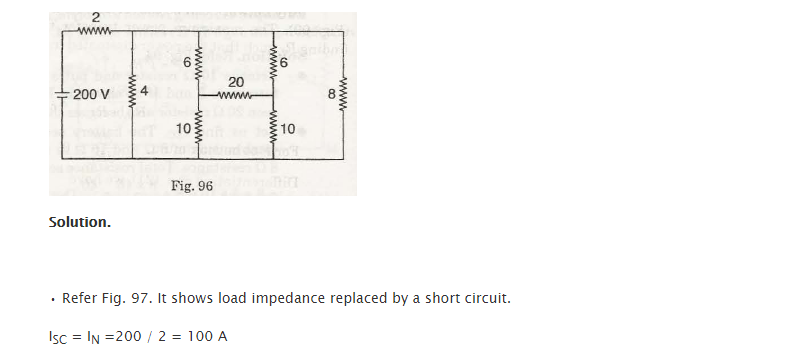
Calculate current value concluded through a load of B Q of the circuit Using Norton’s theorem in the figure 98.
Solution
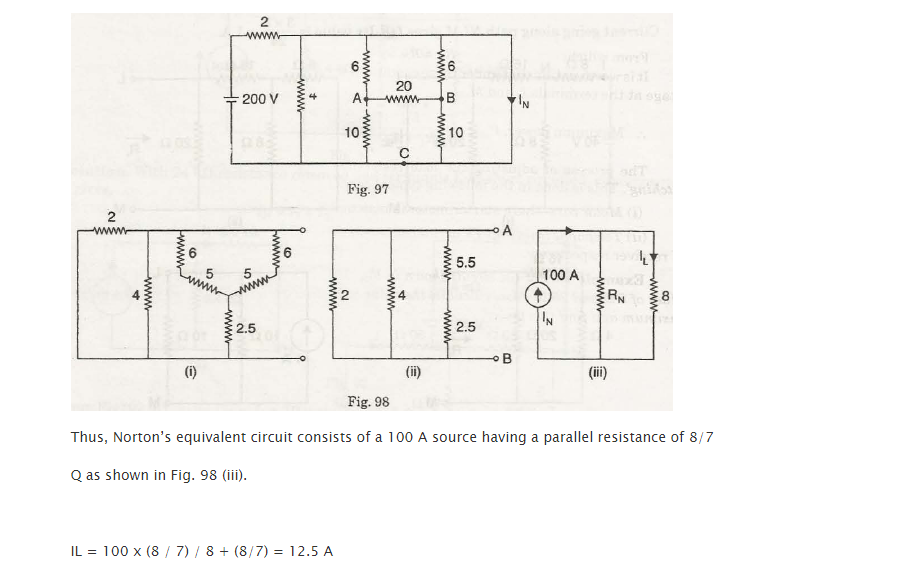
We can see in the figure 97 that load impedance is replaced by the short circuit
We have to replace the △ABC by the equivalent star to calculate RN which is the Norton’s resistance found in the terminals which are open in the figure98.
As noticed RN = 8 / 7Q
Therefore, we can say that similar circuit of Norton includes a 100 A source with the parallel resistance equal to 8/7
Link of Previous Main Topic:-
- Current Electricity Basic Concepts
- Definitions of Important Tenns Relating Network
- Limitations of Ohms Law
- Kirchhoffs Laws
- Applications of Kirchhoffs Law
- Source Conversion
Links of Next Electrical Engineering Topics:-