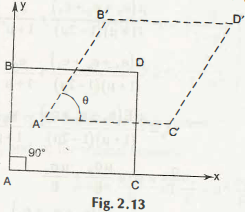
If the faces AB and AC are two adjacent faces and perpendicular to each other, and along with that they are also perpendicular to the x axis and y axis. Just after deformation the AB sides take place of A’B’ and AC side takes place of A’C’. Now, the angle formed by B’A’C’ is not perpendicular or 90˚. It means shear strain can be defined as the angle less than 90 degree. Thus, Yxy = 90° – θ. This is the angle subtracted from 90 degree and this is the value of shear strain.
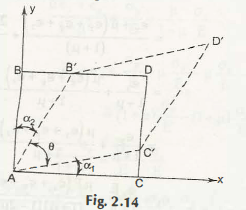
Now, if you consider this in a different way, suppose the displacement takes place from B to B’ in the x direction and C to C’ in y direction, then
The value of shear strain can be provided as Yxy = 900 – θ
= (a1 + a2)
Now, you can easily distinguish between the different conditions to find out the shear Strain.
Links of Previous Main Topic:-
- Rectilinear motion in kinetics of particles
- Work and energy
- Linear momentum
- Force mass acceleration
- Simple stress introduction
- Normal strain
- Stress strain diagram ductile material mild steel
- Axial deformation
- Deformation of a bar due to stress developed
- Poissons ratio
- Shear strain
Links of Next Mechanical Engineering Topics:-