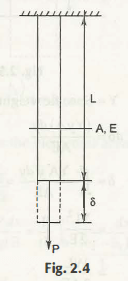
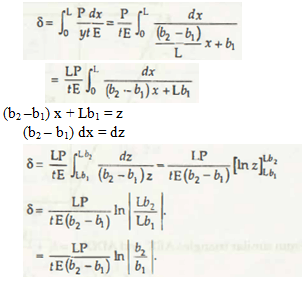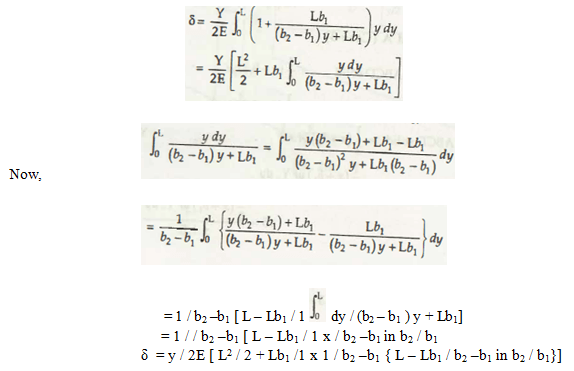The axial deformation is important and to find out you just need to know that Normal stress = σ = p /A
Normal strain = e = δ /L
Deformation can be obtained after knowing the function of A, L, P, E.
What is Hook’s Law?
According to the hook’s law
Stress ∝ Strain or Stress and strain are proportional to each other.
σ = E .e where E is modulus of elasticity and it is constant.
Now, P /A = E x δ / L
- PL/AE = δ
Or δ = PL/AE
At the condition of the constant value of A, P, L and E, the weight of the bar is avoided or neglected.
What are the various cases when constants vary?
At the time of first case when P varies
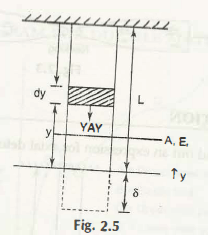
At this condition, the complete weight of the body acts at the exact point C.G. Moreover, the value of its weight varies in other points except C.G. This is for a bar that suspends freely. Now, consider a part of this length as dy. Let that A, E and P do not vary, then the formula δ = PL / AE is applicable here.
Y=specific weight
Dδ = (Yy A) dy / AE
= YL2 / 2E
= WL / 2 AE
δ= WL / 2 AE
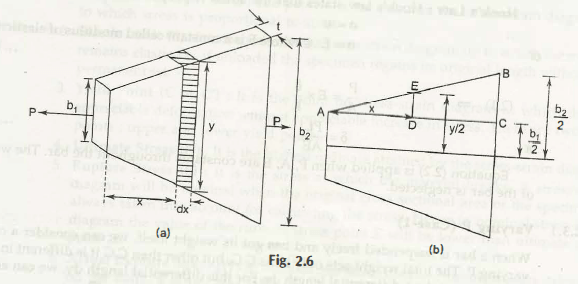
Case 2 at the time Varying A
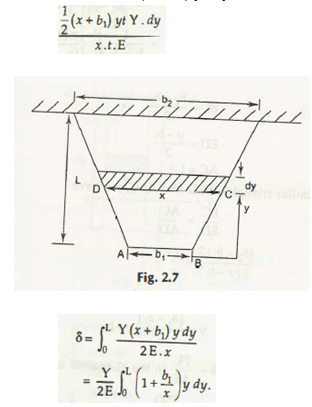
BC = b2 – b1 / 2
ED = y – b1 / 2
AC = L
If you take the similar triangles ABC and AED, then you can easily see that
BC / ED = AC / AD
(b2 – b1)2 / 2 (y-b1) = L / x
y = (b2 – b1) / L x + b1
For the elemental area you can apply for the formula δ = PL / AE.
Now, Dδ = p dx / (yt) E is clear for the elemental area and thus
3rd case when P and A vary
Solid ABCD has the volume =
1/2 (x + b1) ty
Now, the solid ABCD has the weight = 1/2 ( x + b1) yt x y
dδ =
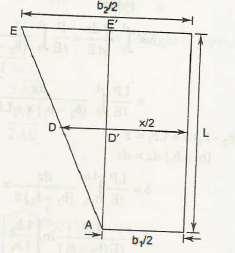
If you go through the similar triangle AEE’ and ADD’, then
x = b1 + (b2 –b1) /L .Y
Now, through the above explanation you can easily get that how deformation takes place and in the different conditions you will get the result in a different way. Thus, be careful about finding out the solution in a proper way.
Links of Previous Main Topic:-
- Rectilinear motion in kinetics of particles
- Work and energy
- Linear momentum
- Force mass acceleration
- Simple stress introduction
- Normal strain
- Stress strain diagram ductile material mild steel
Links of Next Mechanical Engineering Topics:-
- Deformation of a bar due to stress developed
- Poissons ratio
- Shear strain
- Shear stress
- Volumetric strain
- Principle of super position
- Simple strain some definitions
- Working stress and factor of safety
- Statically indeterminate system
- Introduction to thermodynamics
- Statement of zeroth law of thermodynamics with explanation
- Heat and work introduction