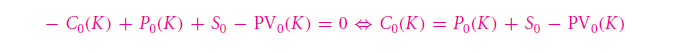Put-Call Parity

One of the most interesting no-arbitrage relationships out there is known as the put-call parity. The most basic used for it is for relating the overall value of an European call with that of a put of the same type. It also takes care of the prices of the stock and the total rate of interest. Take the following example:

• Let, rate of interest = 10% per annum
• Let, current price of stock (S₀) = $80
• European call, along with a strike price = $100 costing a total of C₀ at K=$100, where C₀=$30
• European put which has strike price = $100 costing P₀ with K=$100 where P₀=$50
  

Also, take it into assumption that you have no dividends available to you. And also, since the options available to you are European in nature, you will only really need to take into consideration the amount of payment you have to make now and also what is going to happen during the expiration T. So then, if these are the conditions meted out for you, do you think you can get rich? There is another table listed below which you can use to find the negative outflow.

This table depicts how you can easily sell a single put option for a total of $50 and a shorter one for a different price. You will need a total of $130 in order to purchase one of these calls at a price of $30. At the same time, you need to make a deposit of around $90.91 to your bank thus leaving a free lunch money amount of a total of $9.09.

This is what is known as an arbitrage. However, the good part about all of this is that you do not usually expect something like this to be happening in real life. Obviously, the prices used here are bloated beyond all measures and as such, very unrealistic. Overall however, you can sum up this put-call parity to be something which relates the value of the option for calling to that of a put one, and also vice versa. The formula used for such calculations is given by:

If you observe the options for prices that are listed in the table below, you will find a lot of information that you need to know. The strike price given here listed by IBM is equal to $85 which expires on the 20th of July on 2002. The total amount of interest that prevailed from all of this is equal to 1.77% per year. As such, the strike price which equals to $85 is worth more than just that. The formula used for deriving this is like this:

Solve These:

Q 26.7 Find out the formulary used for finding the put-call parity without using any references from the text above. Also list the inputs taken.

Q 26.8 An option for a single year call has a strike price = $80 with a cost = $20. The share costs a total of $70 while the rate of interest = 10% per annum.

1. What kind of trading should be done for a single year put in option with strike price = $80?

1. How will you be able to earn some more money if your option to put is traded in along with that of the option to call where the price is set at $25 per a single share? Also mention extra details regarding what you want to buy, sell and keep for yourself.

26.2 C  The American Early Exercise Feature

The thing about a put-call parity is that it is applicable only to options which are of European origin. It implies in very suggestive methods that call options of American origin should not be used as much as possible. The reason why that is so goes something like this: If the option for calling is used right now, the price related to the live category of options becomes much more than it should be?It is a given than the worth of the American choice can never be lesser than that of the European one. As such, the call value for the European option is given by something like this:

The formula can be expanded even further in the following manner:           

As such, you can easily guess from the relations depicted above that the American option is always worth something. At the very least, it is equal to everything you will get from immediately exercising it. If you are in dire need of money, you can always get your call sold in the stock market as soon as possible. The table above also shows that you can get an immediate exercise issue from the American option. For instance, on the 20th of July 2002, you can use a strike price of $75 when you will have actually netted a total of $5.50 after exercising the whole thing.

Do keep in mind that the value for your right of exercising something so early equal to absolutely zero. In such a scenario, the value of the American call option is not greater or lesser than that of the European one. As such, you can easily write something like this:

                                                American Call Value = European Call Value

But also keep in mind that there are instances when this kind of early exercising can also be worth a lot. When that happens, the American call value is usually greater than its European counterpart. There are 2 main examples to get this through to you.

Diving Paying Stocks: In any time, if it so happens that the stock lying underneath pays off a dividend that is liquidating in nature, it will definitely be worth more as compared to the holder of the American option to call. This is all of course, before the entire dividend has to be paid off.

Put Options: For example, if you are the owner of a put option that is of 100 years and the strike price which is equal to $1, it is recommended that you collect the total of $99 and go invest the remaining money in someplace else in order to earn more interest. Keeping in mind that your stocks tend to appreciate, waiting for a total of 100 years will inevitably reduce your payoff overall.

Solve Below

Q26.9: What are the conditions under which a Europe call is worth more than an American one?

Q26.10: Try to compare the values of exercising a put option with an American origin to that which is used in a put-call formula. When is it so that the American option to put is better to be used?

Links of Previous Main Topic:-

• Introduction of corporate finance
• The time value of money and net present value
• Stock and bond valuation annuities and perpetuities
• A first encounter with capital budgeting rules
• Working with time varying rates of return
• Uncertainty default and risk
• Risk and return risk aversion in a perfect market
• Investor choice risk and reward
• The capital asset pricing model
• Market imperfections
• Perfect and efficient markets and classical and behavioral finance
• Capital budgeting applications and pitfalls
• From financial statements to economic cash flows
• Valuation comparables financial ratios
• Corporate claims
• Capital structure and capital budgeting in a perfect market
• The weighted cost of capital and adjusted present value in an imperfect market with taxes
• What matters
• Equity payouts
• For value financial structure and corporate strategy analysis
• Capital structure dynamics firm scale
• Capital structure patterns in the united states
• Investment banking and mergers and acquisitions
• Corporate governance
• International finance
• Options and risk management
• A call and put options on stock

Links of Next Financial Accounting Topics:-

• Put call parity
• Valuing options from underlying stock prices
• The black scholes inputs