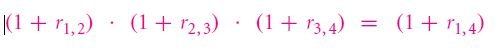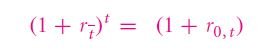WORKING WITH TIME-VARYING RATES OF RETURN

In practical, the rate of return is different from the theoretical value, which depends upon the time of payment. The rate of return also depends on whether the bonds are short-termed or long-termed.

5.1 A    HOW TO COMPOUND DIFFERENT RATES OF RETURN

Let us take an example to understand this. Say, the rate of return of the 1^st year is 20% and the rate of return of the 2^nd year is 30%, then what will be the 2-year holding rate of return? This can be determined by using the two 1-year compounding formula as given below:

Putting r_{0, 1}=20, r_{1, 2} =30, we get r_{0, 2} =56%.

The compounding formula is not applicable only for a period of two years. It can be used for determining the holding rate of return in the future. For example, let us assume that the 1-year rate of return is 30% from 1^st year to 2^nd year, 40% from 2^nd year to 3^rd year, and 50% from 3^rd year to 4^th year, then the holding rate of return for the next 3 years, starting from next year is giving by:

Putting the values, we get r_{1, 4} = 173%. Say, if your investment is $1, then at the end of three years, you will receive $1 and an extra of $1.73 dollar, making the total amount received equal to $2.73.

The rate of interest which begins from the present moment, denoted by a 0 subscript are called spot rates and the interest which begins in the future are called future rates.

REVIEW QUESTIONS

1. Find the total interest rate when the first year interest rate is 2% and it is 3% for the second year.
2. A 2-year project has returned 22% in its 1^st year but overall it has lost half of its value. Calculate the rate of return after the 1^st
3. The year and the annual rate of return of S&P 500 of year has been given in the table. Study the table given below and answer the question:
   

Find the rate of return over the first six years and the second six years. Also, calculate the rate of return over the entire period of 12 years.

4. There are a loss of one-third of the value of a project in the 1^st year, in the 2^nd year it gained 50% of its value and in the third year, it lost two-thirds of its value, and finally in the 4^th year, the value doubled. Calculate the rate of return over the entire period.

5.1 B   ANNUALIZED RATE OF RETURN

An easy way of measuring the interest accumulated by money over a period of time,is estimated by considering the average annual rate of return, which is defined as annualized rates.

Let us understand this by taking an example. If the holding rate of return is 173% over a period of three years, the annualized rate of return will not be given by 173%/3, i.e. 57.7%. This is because this value ignores the compound interest calculated on the interest earned after the first and second years. Instead, a single hypothetical rate of interest needs to be found out which is given by . This equation is given by

Where the holding rate of return, r_{0, t} is for a period of 3 years and hence r_{0.3 is} 173% as per the example taken. We need to find the annualized rate of return . This is given by the following generalized formula:

It should be noted here that compounding is analogous to adding and annualizing is analogous to averaging.

REVIEW QUESTIONS

5.A value is earning interest at the rate of 5% over four months. Calculate the annualized rate of return.

6.If the two-year holding rate of return is 40%, then, the average rate of return is 20% per year. Calculate the annualized rate of return and compare it with the average rate.

7. Give your answer with reasons whether the compound rate is lower or higher than the sum of the individual rates of return, and also whether the annualized rate is lower or higher than the average of individual rate of return.
8. For five years, if the total holding rate of interest is 50%, then calculate the annualized rate of return.

9.For each of the next five years, if the rate of interest is 10% per year, find out the annualized 5-year rate of return.

5.1 C   RELATION OF PRESENT VALUE AND TIME-VARYING INTEREST RATE

The net present value of the time-varying interest rate is given by:

Where NPV is the net present value and PV is the present value of that particular year which is given in bracket.

 

Links of Previous Main Topic:-

• A first encounter with capital budgeting rules
• Stock and bond valuation annuities and perpetuities
• The time value of money and net present value
• Introduction of corporate finance

Links of Next Financial Accounting Topics:-

• Inflation
• Study of treasury bills and yield curve in time varying interest rates
• Why is the slope of yield curve upward
• Corporate insights about time varying costs of capital obtained from the yield curve
• Extracting forward interest rates
• Shorting and locking in forward interest rate
• Bond duration
• Duration stability
• Duration hedging
• Continuous compounding
• Institutional knowledge about compounding and price quotes