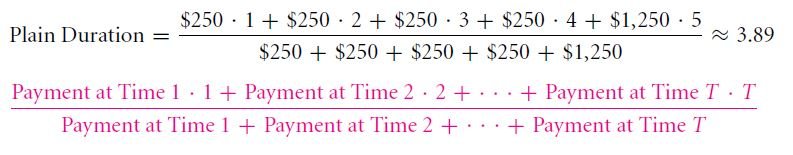The duration of a bond is given by its maturity. If a zero-bond or a coupon bond have the same period of maturity, it might be possible that the coupon bond pays a greater amount of money earlier than the zero-bond does. In order to calculate the payout period of a bond, two factors are taken into consideration-maturity and duration. Duration means the effective time-length of a project. Time weighted average of the bond payouts is calculated, which is then divided by the sum of all payments. Let us take an example. If a 5-year coupon bond pays $250 for four years and $1,250 in the fifth year, then the duration is coming out as 3.89 years, which is explained below:
A physics analogy can be used for explaining bond duration. Let us suppose that payments are weights which are hanging from the time line. The point where all the weights balance out so that the line is shifting neither to the right nor to the left is called the duration point. It has been illustrated below:
Macaulay duration is another process of finding out the duration period. It is the most common duration measure which is used in the real world. It uses the present value of the payouts and make use of the yield curve. Say, if the interest rate on all the horizons is 5%, Macaulay duration of the coupon bond will be given as
REVIEW QUESTION
- The cost of a 2-year bond is $25,000. At the end of 1st year, the interest is $1,000 and the interest received at the end of the 2nd year is $1,000. The principle amount is also repaid at the end of the 2nd
- Calculate the plain duration.
- What is the Macaulay duration if the yield curve is flat 0%, 3% and 10%, respectively?
Links of Previous Main Topic:-
- Working with time varying rates of return
- Inflation
- Study of treasury bills and yield curve in time varying interest rates
- Why is the slope of yield curve upward
- Corporate insights about time varying costs of capital obtained from the yield curve
- Extracting forward interest rates
- Shorting and locking in forward interest rate
Links of Next Financial Accounting Topics:-