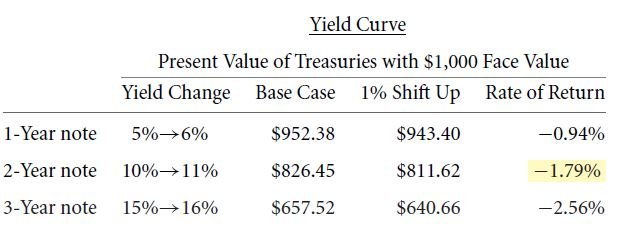
Duration is applicable only on positive incoming cash flows. Risk of the change in interest rate can be calculated by duration. Let us take an example. The yield curve of zero notes is 5% for 1-year, 10% for 2-year and it is 15% for 3-year. A project costing $2,500 can be purchased which delivers $1,000 in 1 year, $1,000 in 2 year and $1,500 in 3 year. The YTM is 17.5% with a Macaulay duration of 2.01 years and therefore the present value of the project is $2765.10 and therefore the project is a good deal. But, if the interest rates increase four times, the project will suffer loss. Now, if the yield curve mentioned before becomes 6%, 11% and 16% instead of 5%, 10% and 15% respectively, the present value and the rate of return will be:
The change in the value of the zero notes due to their change in the interest rates is as follows:
From the table, it can be concluded that the change in the project’s value is most similar to 2-year value. This tallies with Macaulay’s duration of 2.01 years.
Links of Previous Main Topic:-
- Working with time varying rates of return
- Inflation
- Study of treasury bills and yield curve in time varying interest rates
- Why is the slope of yield curve upward
- Corporate insights about time varying costs of capital obtained from the yield curve
- Extracting forward interest rates
- Shorting and locking in forward interest rate
- Bond duration
Links of Next Financial Accounting Topics:-