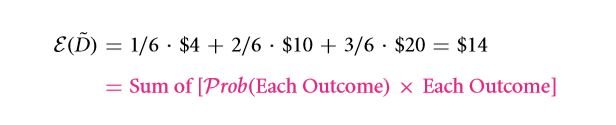Promised versus expected Returns and Debt versus equity in a risk – neutral world
Most individuals of the modern era pretend that they reside in a market that is perfect and doesn’t call for any sort of variation in opinions, taxes, transaction expenses, etc. In addition to this, you ought to find numerous investors and firms or at least you would like to pretend so. This modern era has made the world quite uncertain and as a result, you must abandon idealizing any situation. Though even in this era, the net present value is of utmost importance, however, you ultimately ought to come across the harsh truth that you can no longer use it easily.
This era of uncertainty often leads to situations where in individuals end up getting more cash than they had expected. On the other hand, the same person might come across situations where in he or she gets less cash than what he or she had expected. This is what makes it all the more important for individuals to be able to distinguish between the expected and the promised returns.
As this world is becoming more and more uncertain, this uncertainty factor has paved the way for various additional realism and complexities. Though most of you would assume that it is the idea of NPV that makes it so difficult, but that’s not the case. What is actually difficult to estimate is that cost of capital and the cash flow.
This chapter ought to be focusing on two important topics on finance once it has provided its reader with a suitable statistical explanation so that one can easily understand what is to follow. The first topic that ought to be explained under the scope of this chapter is the interest that lenders should charge borrowers in the event that there exists the slightest possibility of default. Secondly, this chapter ought to provide its readers with a brief idea of two important blocks as far as finance is concerned, equity and debt.
6.1 An Introduction to statistics
Statistics is often considered to be an extremely difficult subject but for those who have placed any sort of bet in the past, there is a high probability that he or she already has a fair bit of idea as far as the subject is concerned. As far as the various foundation science subjects of finance are concerned, statistics is known for being the most difficult of the lot. You must have already heard about the term “expected” but it is under the scope of this chapter that you ought to realize the real essence of the term.
Listed below are certain key aspects of statistics that ought to be highlight under the scope of this chapter:
- It characterizes the uncertain world.
- In the event that the random draw is repeated quite often, the expected value is equal to the average outcome.
- The expected value might not be the probable realization.
- A number who realization is not certain yet is often referred to as a random variable.
- They are nothing but a distribution statistically.
- The probability weighted sum of all the possible outcomes is called expected value.
6.1A Random Variables and Expected Values
If you are in the field of statistics, it is imperative for you to be aware of the term “expected value”. If you have n number of possible outcomes, the expected value is the probability – weighted average of n outcomes. In other words, the term is synonymous to average or mean. The only difference lies in the fact that the terms “mean” and “average” are used if an individual is working with past events while “expected value” deals with future estimations. Let us take into account a simple example. The expected value need not always be a possible outcome. If you consider the activity of tossing a coin, there are two possible outcomes, heads and tails.
Suppose an individual’s receives $1 if the result is heads and $2 if the result is tails, i.e. there is a 50% chance of the individual receiving $1 and 50% chance of the individual receiving $2. Hence, under the stated circumstances, the expected value of each coin toss is equal to $1.5. If an infinite number of coin tosses are taken into consideration, it is found that the mean of the actual outcomes often referred to as realizations coincides with the expected value, i.e. $1.5.
NOTE: In the event that you consider infinite number of events, the expected value is found to be equal to the average or mean.
In order to make the task of working with the uncertainties, professionals in the field of statistics have come up with the concept of random variable. It is another term which is extremely important as far as statistics is concerned. The random variable is a variable whose outcome is yet to be calculated. If you consider the coin toss experiment, you make declare a random variable, say c. This variable c takes the values $1 and $2 with 50% probability each. In this case, the expected value of c is equivalent to $1.5.
Once the coin toss event has occurred, the actual outcome often referred to as c can be $2. The random variable c, is no longer the random variable upon the occurrence of the event. The expected value is denoted by the symbol Ɛ and to denote a random variable the tilde sign (~) is used over the variable. The tilde is removed once the event has occurred. A question that pops up more often than not is whether or not the expected outcome is a random variable? Well, the answer to this question is obviously NO! The expected outcome ($1.5 in case of the coin toss) is calculated way before the event has occurred.
The expected value is often thought of as a non – random variable. On the other hand, if you consider the possible outcome, it is without a doubt a random variable. The expected value and the actual outcome may overlap in the event that there is only one possible outcome of a particular event. Under such a circumstance, the non – random variable also overlaps with the random variable.
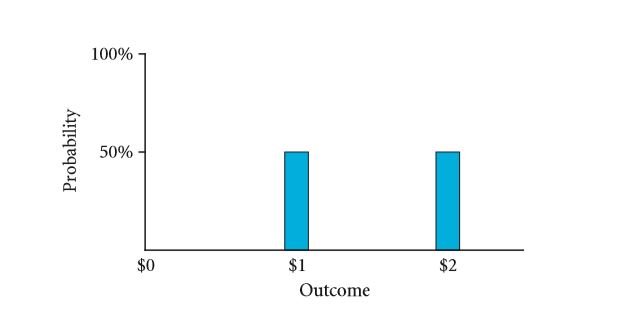
FIGURE 6.1: A Histogram for an event with two possibilities having equal probability of occurrence
Suppose the event has occurred and the outcome comes out to be heads. Now the question that arises is whether or not this heads is a random variable? Well, it isn’t! Once a head comes up, it is an actual outcome. This heads is no longer random.
A variable that can be defined by the distribution of probability of its possibilities is often referred to as a random variable. The probability distribution is extremely simple if you consider the coin toss example where the chances of the value $1 and $2 are same and equal to 50% each. The FIGURE 6.1 shows the probability distribution for a coin toss. In a histogram, the possibilities are marked along the x – axis and the probabilities are marked along the y – axis.
A major assumption that must be considered as far as this chapter is concerned is that most of the situations are considered to be uncertain. The random variable is often thought of as the placeholder as far as the FIGURE 6.1 is concerned. Another thing about this chapter is that the assumption of the perfect market is still not eliminated.
Individuals often wonder as to why there are no disagreements with the assumption. In brief, it refers to the fact that individuals must have consent on the probabilities of the possibilities. If you consider an event similar to the coin toss event wherein the probability of getting $1 is 51% and that of getting $2 is 49%. Such a market can be considered to be an imperfect market.
Fair Bets
Fair bet is a term that is used in the field of finance more often than not. It is used to refer to a bet whose cost is equal to its expected value. For an infinite number of tries both the individuals taking part in a bet ought to end up having the same number of wins. Suppose D is the playoff of an individual and it is based on the following rules:
- You have a probability of 3 / 6 that you will get $20.
- A probability of 2/6 that you will get $10.
- A probability of 1/6 that you will get $4.
If the playoff if uncertain, it falls under the category of random variable which is often referred to as ˜D. suppose this structure is stimulated by throwing a die according to the following criterias:
- You get $4 if one comes up.
- You get $10 if two or three comes up.
- You get $20 if four, five or six comes up.
If the above criteria’s are meet, will the bet have a fair price? If yes, what is it? To begin with, Ɛ (~D) must be determined in the following way:
In the event that an individual repeats this experiment a zillion number of times, he or she might as well end up earning $14 zillion. If the number of tries is large and if you consider your average earning per try, it would be about $14. However, in case of a real life experiment, the number of trials is finite and as a result, the average earning would be slightly more or slightly less than $14. However, it ought to be fair if and only if the cost of a single bet is $14.
The approach taken for computing the expected value is quite common. It is equal to the sum of the products of the probability of the outcome and the outcome. The expression is given below:
A simplified version of the approach taken above is given below:
NOTE: This expression is general and as a result, it works even with impossible outcome. All you need to do is assign a probability of zero to them.
NOTE: Here are a few things that you must note before proceeding with this chapter:
- Difference between an expectation and realization.
- The marginal difference that exists between a random variable and an ordinary variable.
- The real idea of a fair bet.
- The procedure for calculated the expected values using the outcomes and their corresponding probabilities.
Exercise
Q 6.1 Can the expected value be a random variable for any bet?
Q 6.2 A stock has the following probability distribution:
If the cost involved is $50. Discuss whether the investment is a fair bet or not?
Q 6.3 State whether or not the expected value of a die throw can be considered to be a random variable?
Q 6.4 Consider a die throw that had a six as its result. Discuss the experiments expected outcome before the experiment was carried out and its realization.
6.1 B Variance and Standard Deviation
Variance and standard definition are two very common terms that are used in finance. The need for measuring the average outcome often arises at the time of making any sort of investment. Another thing that individuals must figure out is the summary measures. These measures are carried out on manner in which the possibilities are spread out. Normally the expected value is used as the measure.
Another characteristic of investment that needs to be measured more often than not is risk. In the event that you wish to move onto the next few chapters, these two ideas definitely ought to play a huge role as they ought to be discussed in details there.
As of now, all you need to know about risk is that it is a measure of the manner in which the outcomes tend to vary based on the expected mean. Standard deviation is perhaps one of the most common measure of risk. Standard deviation is equal to the square root for sum of squares of the value of deviation from mean. Let us take the dice problem again.
Firstly, we must find the square of the value of the deviation from the mean.
For the first case:
Outcome = $4
Mean = $14
Deviation = $4 – $14 = – $10
(Deviation) 2 = (-$10)2 = +$$100
NOTE: Dollar square is a strange unit and it is not possible to interpret. Hence, it is recommended for individuals to not even try this.
For the second case:
Outcome = $10
Mean = $14
Deviation = $10 – $14 = – $4
(Deviation) 2 = (-$4)2 = +$$16
For the third case:
Outcome = $20
Mean = $14
Deviation = $20 – $14 = + $6
(Deviation) 2 = (+$6)2 = +$$36.
In the next step, you must determine the expected value of the deviation squares that has been calculated above. This is sometimes called variance
The SD or Standard Deviation is:
Thus, the promised results have been produced. The standard deviation is found to be the root over of the mean of the square of deviation from the average. Though the variance has units that is impossible to interpret, the unit of standard deviation can be implemented. Thus, you can see how the standard deviation and mean can be used to characterize the bet of an individual. For the adopted example, the outcome ought to be equal to $14 (the expected value) minus or plus $6.32 (the Sdv (…)).
Exercise
Q 6.5 Find the risk (the Standard Deviation) for the investment from Q 6.2 of its outcome P + 1.
6.1 C Risk neutrality and preview of risk aversion
Assuming risk neutrality refers to the act of choosing investments based on the expected value. As far as the scope of this chapter goes, the expected value is all an individual needs to know about. This is due to the fact that we have made an assumption that everyone is risk neutral. This assumption is made for the sole purpose of learning.
The investors are mostly ready to take or write any bet that is fair. If a risk neutral individual is considered, it is observed that he or she would be indifferent between winning $1 for certain and getting $0 or $2, each of these having a probability of ½. In other words, the individual may be indifferent between earning 0% or 20% and earning 10% without taking any form of risks. There doesn’t exist any sort of preference in the mind of such an individual regarding investments based on the safety or uncertainty of these investments.
On the other hand, if you consider risk adverse individuals, such individuals will without a doubt prefer the safer option neglecting the extra bit of income that they may receive. If you consider the above example, such individuals ought to go for the $1 option without going for the $0 or $2 option.
If you consider the Treasury bond and the corporate bond which offers 10% and 0% or 20% respectively, you would certainly go for the Treasury bond. In the event that I want to offer such an individual with a more risky option, I must make sure that a much higher expected value makes up for the extra amount of risk involved.
Another aspects about risk adverse individuals is that they don’t prefer accepting fair bets. This behavior is often considered to be a definition for risk aversion. For small bet amounts most individuals are nearly risk neutral, i.e. for a bet of either – $1 or + $1 one certainly won’t worry much.
In case of a risk adverse individual, I might as well offer a temptation of 5 cents in order to make a client go for the $0 or $2 option where a risk free $1 option is already available. This however, is the case with big bets only. In addition to this, individuals must also try to bring down the price of the corporate bond so as to increase the expected rate of return.
Let us now consider a bet of + $ 100 / – $ 100 or + $10,000 / – $10,000. Under most circumstances individuals ought to opt for the 2nd option without any sort of risk bearing compensations. As far as the investors are concerned, the degree of risk aversion is directly proportional to the bet amount.
As far as tempting an individual to go for the + $ 10,000 and – $10,000 bet is concerned, the incentive may rise to several hundreds of dollars. If an individual considers a real life scenario, he or she ought to figure out that the difference between the expected and the promised values are a lot more important than the risk compensation amount.
Risk aversion ought to be discussed in details in the next chapter. However, as far as the scope of this chapter is concerned, it will be focusing on the pricing mechanisms considering the risk factor to be neutral. However, the things that have been explained are applicable for risk averse individuals as well.
In the event that you are taking financial marketing into account, it is for certain that your own personal risk aversion isn’t that important. The major reason behind this is the idea of risk sharing.
The price investments in the financial sectors are often similar to the aggregate risk aversion which can bring quite a bit of revenue. Going back to risk sharing, if the $10,000 bet is sharing with 10,000 other individuals, you own risk (i.e. the individual risk will only be + $ 1 or – $ 1). Some of the individuals with whom you are sharing the risk may be willing to take more risk. In the event that an individual considers taking bets across various investors, the effective risk aversion is quite low.
This is the exact manner in which the financial market goes about their propaganda. The aggregate of the risk absorption capabilities of the market is higher than that of individual investors, i.e. the market is less adverse towards the risk factors involved in a particular bet.
Anecdote
The Ruin of the First Financial System
If you consider the widest as well as the earliest known example of financial default that took place in the 1788 B. C. E., the royal edit was responsible for destroying an entire system of flourishing finance and commerce. It was during that time that the King of Uruk (Mesopotamia) King Rim – Sin cancelled all repayments. The system destroyed was more than a thousand years old. However, till date the reason behind this is known.
Exercise
Q 6.6 Compare the risk aversion of investors for small and large bets. Should the investor wealth be considered relatively while defining “small”?
Q 6.7 Compare the risk aversion of investors and individual investors.
Links of Previous Main Topic:-
- Working with time varying rates of return
- A first encounter with capital budgeting rules
- Stock and bond valuation annuities and perpetuities
- The time value of money and net present value
- Introduction of corporate finance
Links of Next Financial Accounting Topics:-
