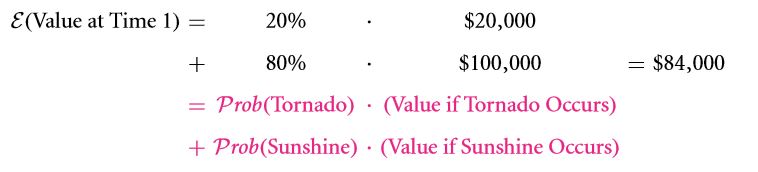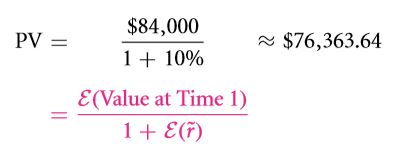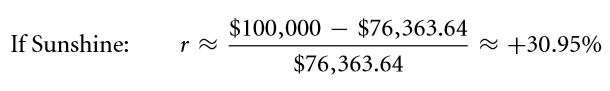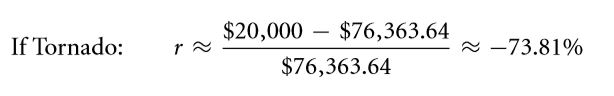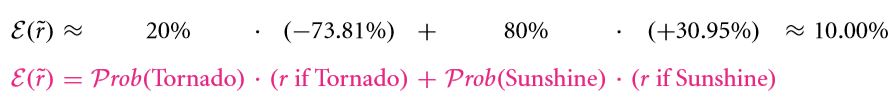The next thing that ought to be discussed in details under the scope of this chapter is a playoff diagram. This out to come in handy at the time of characterizing future contingencies. This section of the chapter will be revolving around the various tasks that are an integral part of capital budgeting. Another major task here is choosing a particular project under various uncertainties. You will receive a pay off or a state table using which you have to compute the present value.
This present value ought to be computed with knowledge of future outcomes that are imperfect. This table considers various scenarios and probabilities are assigned to corresponding projects. The manager of a company is the individuals responsible for making the payoff table. If you consider a factory that manufactures hard disks. The company’s economy ought to depend on whether computer sales are low or high, which products have become obsolete, etc.
Another major factor that needs to be considered is the price of oil which is without a doubt an extremely important cost factor, i.e. transportation. Understanding the key factors is perhaps the most important part. In addition to this, assigning probabilities considering the various key factors. In the event that the individual wishes to figure out how to assess their own project, he or she ought to be very precise.
For figuring out the worth of a project, its key areas must be determined. Though all the minute outcomes of a particular project need not be described. Considering a handful of scenarios ought to be sufficient. Describing all the outcomes minutely isn’t that easy a task.
6.3 A Present value with state-contingent payoff tables
Before we progress any further with this chapter, let us imagine a purchase of a building and let us consider that the future value of this building is uncertain. Take the current time to be time 0. The present value of the building must be determined and it ought to stay till next year (=time 1). In addition to this, let us assume that there is a probability of 1/5 that the building will be destroyed within time 1 may be by a tornado.
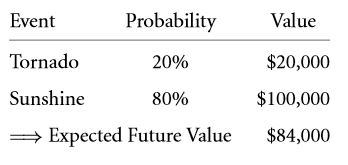
If the building is destroyed by the tornado, then the only remaining worth will be the value of the land which would be round about equal to $ 20,000. So, the probability of the worth being $100,000 at time 1 is 4 / 5. The market value of $100,000 will without a doubt depend on various other factors mostly any sort of modification made inside the home.
The real estate evaluation must also be made. Another capitalized value must be considered that is concerned with the probability of the occurrence of the storm the following year.
The Building’s Expected Value
Considering that an individual owns an entire building, his or her pay off table will look somewhere close to the following table:
In order to compute the expected value of a building in future, the following approach must be taken:
Each possible outcome is multiplied with its probability. Then the value is again discounted with the help of an apt cost of capital. Consider a project falling under the category of building having a maturity of 10% (this may be supplied in the field of finance as a result of the various demands and supplies) for a year and a risk as above.
The correct return rate for the above must be calculated. This is definitely known to the manager. The purpose of a manager is to find the correct price of the building and there are two roads that can be taken.
If you have gone through the chapter thoroughly you will definitely find the ways quite familiar. The first road is the PV approach. It can be used to compute the expected value of a particular building. In addition to this, it can be discounted as well.
All an individual needs to do in this case is replace the future return rate and the known value with the expected return rate and the expected value respectively. The 2nd road focuses on finding the state-contingent value (discounted) of the property. Once this is done, the previous table is augmented to find the expected values.
The present value of the building ought to be $ 18,181.82 in the event that the tornado actually strikes. On the other hand if the tornado doesn’t strike, it ought to be $90,909.09. Therefore, the expected value can be found using
Irrespective of which approach you take, you ought to end up with the same result. Firstly, the expected value of the following year can be computed in the following manner:
- 1/5 of $20,000 + 4/5 of $100,000 = $ 84,000.
Next, $84,000 the expected value must be discounted and the value $76,363.64 is obtained.
In the second approach, all the possible outcomes for the future is discounted
- Example: $ 100,000 may be discounted to $ 90,909.09 or $ 20,000 can be discounted to $18,181.82.
Then the expected value is computed from the values obtained after the discount has been applied.
- 1/5 of $18,181.82 + 4 /5 of $90,909.09= $ 74,363.64.
Note: The order in which you carry out taking expectations or discounting doesn’t actually matter. Any order can be followed the result is the same. The NPV formula is:
- Changed by replacing the appropriate expected return rates in place of appropriate return rate.
- Changed replacing the future cash flow with expected cash flow that has been discounted.
The State-Dependent Rates of Return
Two questions still remain, the rate of return and the expected return rate under both the circumstances, i.e. the tornado strikes and the sun shines.
When no tornado has struck:
Price of building= $ 76.343.64
Now, considering the scenario where in the tornado has struck:
Thus the, expected return rate can be computed as:
In the above example, the expected return rate of 10 % has been used to find the price of the property. The probability of the return rate is weighted are used to obtain the return rate.
Exercise
Q 6.12 Considering you have an uncertain condition in hand, how should you modify the NPV formula so that it can be used to solve the problem?
Q 6.13 The probabilities of a factory being worth $ 1,000,000 or $ 500,000 after an interval of 2 years is equal with a capital cost of 6 %. These probabilities are strongly dependent of the future demand for the products. Calculate the value of the factory at present.
Q 6.14 Suppose a company is launching a new product and the demand of the product in the market will be as per one of the following:
- 20 % probability of the product being a dud.
- 70 % probability of the product being an average seller.
- 10 % probability of the product being a super hit.
The corresponding payoffs will be $ 20,000, $ 40,000 and $ 80,000 respectively. Find:
- The expected return rate where the payoff is equal to 8 %.
- Find its PV.
- Consider that I purchase the product at the correct value. That return rate can I expect under the 3 conditions that are listed above.
- Find the product’s expected payoff.
Links of Previous Main Topic:-
- Introduction of corporate finance
- The time value of money and net present value
- Stock and bond valuation annuities and perpetuities
- A first encounter with capital budgeting rules
- Working with time varying rates of return
- Uncertainty default and risk
- Interest rates and credit risk default risk
Links of Next Financial Accounting Topics:-