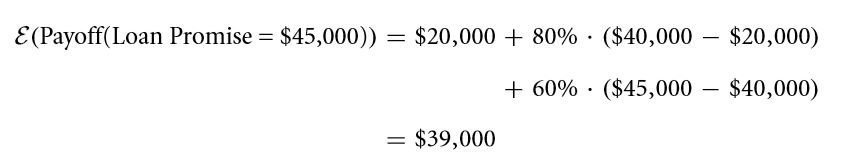Q 6.20 Consider the example with 5 possibilities and a promised value of $ 45,000 compute the value of the expected pay off.
Q 6.21 If the building value is distributed normally, i.e. there are infinite number of outcomes, plot the graph for the expected vs the promised payoffs.
Q 6.22 Consider a situation where in the probabilities of the possibilities are not same. $ 20,000 has a probability of 12.5 %, $ 40,000 has a probability of 37.5 %, $ 60,000 has a probability of 37.5 % and $ 80,000 has a probability of 12.5 %.
- Compute expected payoff if the promised payoff is $ 50,000 for a particular loan.
- Represent figure 6.4 in the form of a graph.
- Take the rate of return to be 5 % before a particular payoff and you need a loan of $ 25,000, find the promised payoff. Also calculate the rate of interest.
Q 6.23 Consider the expected payoff for the example with five possibilities to be $ 45,000. Compute the promised payoff.
Q 6.24 Compute the exact value where the expected payoff and the promised payoff are $ 38,500 and $ 45,000 respectively.
Q 6.25 If payoffs of $ 60,000 and $ 80,000 were promised, find an equivalent formula of 6.1.
Q 6.26 Consider an expected return rate to be 6 % / year. The probability of a new product being a hit, an average sale and a dud is 1 / 10, 7 / 10 and 1 / 5 respectively and the corresponding payoffs are $ 80,000, $ 40,000 and $ 20,000 respectively. Find the expected and the promised rates of return if the promised payoff is $ 40,000.
How Bad Are Mistakes?
Discounting promised cash flows with the promised cost of capital
Two errors cancel out each other. Well, if you are in the field of finance, there’s absolutely no way in which you can have such a mindset. However, if the need to compute the expected value arises, the discount rates and the cash flows can easily be adjusted. The discount rates are used to discount the cash flows as both are synonymous to the same risk. In order to illustrate, let the proper expected return rate be 10%.
A bond Investment which has been recommended might assure to provide $16,000 for an investment of $100,000, but there will be by default a risk on the interest rate of 50% being offered(the principal sum has been insured). Your standard guaranteed prospect price of principal will rely on uncertain bonds that possess unavoidable premiums of 2%. At times, individuals might as well end up with a present or current value that is nonsensical. Consider the values + $ 116,000 / 112 % −$ 100,000 ≈ +$3,571 nor $ 16,000/112 % + $ 100,000 / 110% − $ 100,000 = +$ 5,195, neither of them ought to be equal to the NPV of your project.
A thing about this bond is that the amount put in may not payoff as expected.
Exercise
Q 6.27 Differentiate between short – standing or during long – standing projects?
Q 6.28 For a project that’s going to take a hundred years, describe the relative significance of cost occurred regarding capital errors and flow of cash.
Q 6.29 For a project that’s going to take 10 years, state the comparative importance of costs incurred due to capital errors and flow of cash?
Summary
This particular chapter has covered the major points given below:
- When speaking of the expected value, it is the probability of the weighted summation of all the probable outcomes. This is a kind of average or mean but it will be provided to the future rather than a series of historical data. It can be referred to as a measure of the reward.
- The meaning of uncertainty is that a particular project may or may not return the amount which has been promised.
- You will see that the probability of rate of interest of default causes is higher than the expected values. This kind of risk is often known as credit risk too.
- With the aid of credit ratings, you can know about the probability of occurrence of future losses. You will see that Moody’s and S&P are the leading vendors providing rating to corporate bonds.
- When probable rates of return of a bet irrespective of whether the bet is safe or risky are same, then the condition is called risk neutrality.
- It has been observed that the major difference between promised rate of interest and expected one occurs owing to the default. There is always additional compensation when more risks are involved. The risk and other such premiums are smaller than the default bond premiums.
- The outcome of a random variable has not been determined yet. This is mainly characterized by the circulation of different outcomes in the future.
- Debt and equity are two of the most common state contingent based claims. The right for payoff is best described using the payoff tables. The payoff tables and several rules associated with it have already been discussed in details under the scope of this chapter.
- The payoff table is the most important tool when it comes to discerning of uncertainty. The different rows represent different possible outcomes. The probability describes whether the state would be coming round to distributing the total value of the project. The entire value of the project would be distributed to various state based contingent claims. These claims actually form payoffs for the projects.
- According to NPV, the expected flow of cash is to be discounted upon, relative to the rates of return expected from transactions. You will not be able to predict results if instead of the discounted cash flows along with rates of return promised originally.
- When it is seen that the debt is able to provide more than the project itself even in the worst case scenarios, then it can be said that the nature of debt is risky and hence the promised interest rates will exceed the expected one.
- The entire risk factor can be given out in one particular component using debt and equity. This is safer than the whole firm when it is debt and vice versa when it is equity.
- NPV can be termed as strong to not so strong errors in the interest rate expected to occur in the flow of cash. You have to understand that NPV is not at all robust when it comes to weak errors in flow of cash which is expected along with the rates of discount in the far off cash flow.
- When debt is present, the investments in equity cranks up. Smaller investments in cash are now subjected to more differences in values. There are lots of mechanisms for leverage that different firms can get hold of.
KEY TERMS
Q 6.1 When an untampered die is thrown, the expected outcomes are presumed to be known by all. This phenomenon can almost be regarded as philosophy and is quite ahead of what you know till now and how you answer: a case may occur when the estimated value of a particular input isn’t known. Hence here it can be treated as a variable that is random in a sense. You are however expected to be having an opinion regarding all things hence it may not be regarded as a variable that is random too.
Q 6.2 In the event that you are not aware of the correct bet being placed, it is quite probable that the value expected of you to know will be at large. This is very well exemplified when it comes to dealing in stocks. The return rate is often guessed out there. However in case of a die you must know the physical process taking place to bring about an outcome. Most of the theories of finance assume that you are aware of the expected values. The theories often hope that you have a fairly good idea regarding the values.
Q 6.3 If a particular arbitrary variable represent the number of dots that are present on a die, then the outcome that be expected is
1 / 6. (6 + 5 + 4 + 3 + 2 + 1) = 3.5
[6 has been taken as the realization value]
Q 6.4 Most of the investors have a certain aversion in placing large bets in correspondence with their health.
Q 6.5 It is often seen solo investors are more averse to risks than those in groups.
Q 6.6 The rate which is expected to be delivered and that which is promised remains constant only for the bonds of the government. There is some default risks associated with all other bonds.
Q 6.7When the probabilities are reversed:
(a) The new payoff is now 95%. $210 + 1%.$100 + 4%. $0 = $200.50. Hence, the likely return rate is $200.50/$200 = 0.25%.
(b) You want an anticipated payoff of $210 in order to finish off with 5%. Thus, you have to answer for a guaranteed payment 95%. P + 1%.$100 + 4%. $0 = $210 ⇒P = $209/0.95 = $220. Upon a loan of $200, this can be regarded as 10% guaranteed rate of interest. Q 6.10 The default premium which is desired by all is zero.
Q 6.8 You will see that statistics have to say that below-grade debtors default way too often and pay up less after defaulting.
Q 6.9 It is seen that the authentic flow of cash is often substituted by the expected one. The rate of return on an annual basis is changed by the expected value.
Q 6.10The expected value of factory is E (Value at Time 2) = [0.5. $500,000 + 0.5 . $1,000,000] = $750,000. The present value is henceforth $750,000/1.062 ≈ $667,497.33.
Q 6.11 When it comes to the dynamite or dud assignment.
(a) The projected payoff is E (P) = 20%. $20,000 + 70%.$40,000 + 10%. $80,000 = $40,000.
(b) The current worth of the probable payoff is $40,000/1.08 ≈ $37,037.
(c) The three different return rate outcomes are $20,000/$37,037 − 1≈ −46%, $40,000/$37,037 − 1≈ +8%, $80,000/$37,037 − 1≈ +116%.
(d) The much expected return rate is 20% . (−46%) + 70% . (+8%) + 10% . (+116%) = −9.2% + 5.6% +11.6% = 8%.
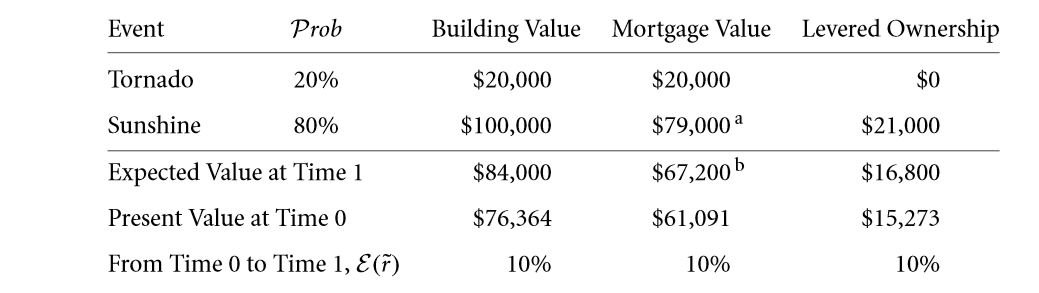
Q 6.12 The partners will have to share the payouts equally and not by the norm that debt comes in the beginning. According to examples in the state of tornado, the 32.74% is going to receive about $6,500 rather than the whole $20,000 that the owner of debt gets.
Q 6.13 The 80% mortgage would be financing 0.8 .$76,363.64 ≈ $61,090.91 today.
- The essential promise of mortgage is (1.10 . $61,091 − 0.2 .$20,000)/0.8 ≈ $79,000.
- The likely mortgage payoff is 0.2 . $20,000 + 0.8 . $79,000 = $67,200.
Q 6.14 When you take rent into account:
- In the state of sun, the worth is $120,000 + $11,000 = $131,000. The tornado state shows, the cost is
- $11,000 + $20,000 = $31,000. Hence, the expected value of building is $111,000. The building value after getting discounted upon presently is $111,000/1.10 ≈ $100,909.09.
- It is quite static and the same as that in the text: The $25,000 loan of lender can yet only fetch $20,000, hence it is regarded as a promise for$29,375. The quoted rate of interest is still 17.50%. $100,909.09 − $25,000 = $75,909.09.
- The value as yet is at $100,909.09, presuming the proprietor believes living inside the particular construction just as much as any given resident would. The rent which is taken up by the owner is almost comparable to the different dividends of corporate nature which are paid off in order to lever the equity. You will also be able to repeat this kind of example knowing that the particular rent is actually an annuity of $1,000 per month. The tornadoes actually strike in the middle of the year.
Q 6.15 The loan which promises to give off $25,000 (rather than providing it): In the state of tornado, the creditor will be getting all of the $20,000 whereas in sunshine state, the creditor will receive the promised sum of $25,000. Hence, expected payoff of the creditor is 20%. $20,000 + 80%. $25,000 = $24,000. In order to offer a projected rate of return of about 10%.
You can get $24,000/1.1 ≈ $21,818 from the creditor today.
(a) Repeating the table:
(b) The loan pays off $21,818 in the present day.
(c) The vowed rate of return for the money is thus $25,000/$21,818 − 1 ≈ 14.58%.
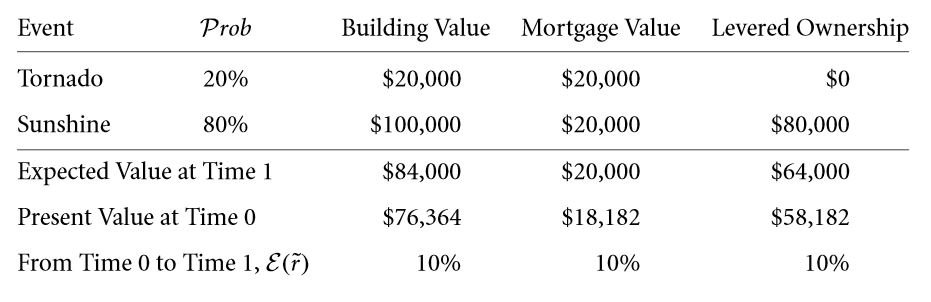
(d) You need to understand that the levered building proprietorship is much riskier than being the owner of full building.
Q 6.16 You will see this particular loan free of risk will be paying off $20,000 surely. The levered kind of ownership pays either $0 or $80,000, and will cost $64,000/1.10 ≈ $58,182. Hence, the rate of the return is either going to be −100% or +37.50%. previously, you have worked out complete ownership here in this particular text: It is going to pay either $20,000 or $100,000, and will cost $76,364, but is not going to offer either of the deals−73.81% or +30.95%. When undertaking inspection, the levered kind of equity project is becoming more risky. As a result of this, ownership of particular concrete buildings have become too risky, this happens because the owner might have chosen to get away from that risk-free element and retain only that very risky section.
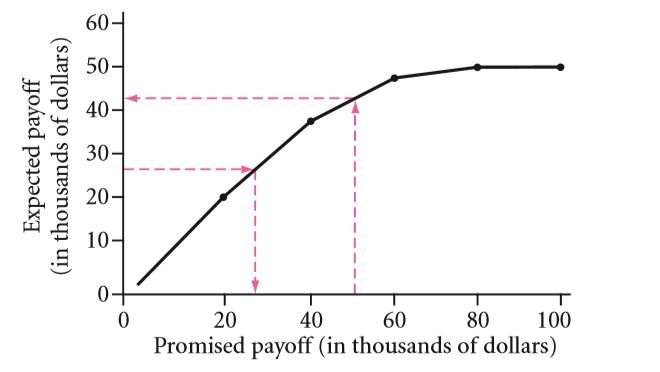
Q 6.17 The presence of many different possible outcomes, the function made for expected payouts would be an evenly increasing function. For all those mathematical geeks: A normal distribution has to have been allowed. The worth of a particular building should not be negative in nature. You will see that the required function increases monotonically in the beginning and eventually becomes an asymptote.
Q 6.18 When viewed from a graph, for a particular promised amount of payment of $45,000, the expected value payoff is about $40,000. The most accurate value will be obtained by going through Formula 6.1 on page 163:
Q 6.19 Seen, from the graph, when the estimated payoff is $45,000, the promised payoff will be about $55,000. The proper worth can be got by putting Formula 6.1 on page 163 equal to $45,000 and answering for “Loan.”
Q 6.20 the presently unequal probabilities provided,
(b) The precise expected payoff will be 1/8 . $20,000 + 3/8 . $40,000 + 1/2 . $50,000 = $42,500. The 1/2 is regarded as that probability that you are going to get the amount $50,000 that you were promised to be given, which will occur if this project completes up to be worthy of at least as much as the promised amount of $50,000. This will mean that the complete probability that is going to be worth between $60,000 or $80,000.
(c) The loan should expect to emolument off (1 + 5%) . $25,000 = $26,250. Hence, solve 1/8 .$20,000 + 7/8.
x = $26,250, so the exact promised payoff must be x ≈ $27,142.86.
Q 6.21 Having a probability of 20%, the loan is going to pay off $20,000; with the coming of 80% probability, the loan will be giving you the complete promised $40,000. Consequently, expected payoff of the loan is going to be 20%. $20,000 + 80% . $40,000 = $36,000. The
Price of the loan is $36,000/1.06 ≈ $33,962. It is hence regarded, that the promised return rate is $40,000/$33,962 − 1 = 17.8%. Hence the expected return rate was given: 6%.
Q 6.22 Once you have reached beyond $20,000 + 0.8 . $20,000 = $36,000 in range of expected value, you will drop into the 3rd part of the function, where you will get only 60% on a given dollar. So, you can of course set Formula 6.1 on page 163 equal to $38,500 and solve for “Loan”:Q 6.23 In order to judge importance of relative error, you have to consider a project that earns $100 in period of 10 years and where the proper rate of interest is 10%.The exact PV is hence $100/1.1010 ≈ $38.55.If the flow of cash is wrongly estimated to be for example 10% higher, the improper PV is $110/1.1010 ≈ $42.41. (This is going to be 10% greater than the accurate value.)
If the rate of interest is improperly assessed to be 10% lower, the wrong PV is $100/1.0910 ≈ $42.24. (This will be 9.6% greater than the true value.)
The effects of miscalculations are soundly similar at rates of interest of 10%. Certainly, percent assessment mistakes in the rates are higher if the rate of interest is greater (and lesser if the rate is lower).
Q 6.24 The precise rate of interest actually determines the comparative importance , hence 100 years is so long that charge of principal errors almost assuredly count for any kind of sensible interest rates presently. The errors in flow of cash is still going to matter and even more when hesitation about forthcoming cash flows rises with the skyline, just as maximum real-world cash flow ambiguity would be.
Q 6.25 The uncertainty of rate of discounts is comparatively more challenging for lasting projects. For temporary projects, the exponents are able to limit the damage incurred.
Q 6.26 Is the present morning’s CNN forecast of temperature of tomorrow an arbitrary variable? Is temperature of tomorrow going to be a haphazard variable?
Q 6.27 Does a greater payment (estimated return rate) will always come with greater risk?
Q 6.28 Would you say that a single individual be efficiently more, alike, or be less averse to risk than a group of such depositors?
Q 6.29 A particular financial instrument is going to emolument off as follows:
(a) What amount in the present day would mark this as a reasonable enough bet?
(b) What is going to be the full amount that an investor averse to risks will be agreeable to pay off?
Links of Previous Main Topic:-
- Introduction of corporate finance
- The time value of money and net present value
- Stock and bond valuation annuities and perpetuities
- A first encounter with capital budgeting rules
- Working with time varying rates of return
- Uncertainty default and risk
Links of Next Financial Accounting Topics:-
- Risk and return risk aversion in a perfect market
- Investor choice risk and reward
- The capital asset pricing model
- Market imperfections
- Perfect and efficient markets and classical and behavioral finance
- Capital budgeting applications and pitfalls
- From financial statements to economic cash flows
- Valuation comparables financial ratios
- Corporate claims
- Capital structure and capital budgeting in a perfect market
- The weighted cost of capital and adjusted present value in an imperfect market with taxes
- What matters
- Equity payouts
- For value financial structure and corporate strategy analysis
- Capital structure dynamics firm scale
- Capital structure patterns in the united states
- Investment banking and mergers and acquisitions
- Corporate governance
- International finance
- Options and risk management