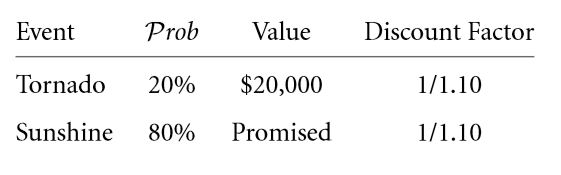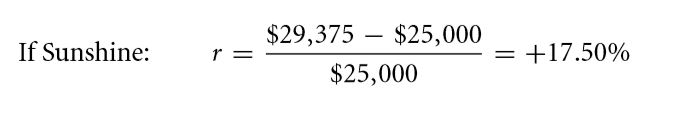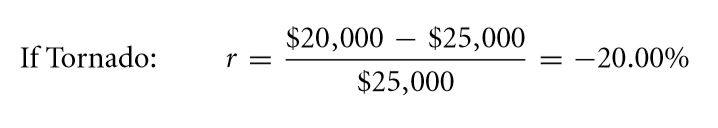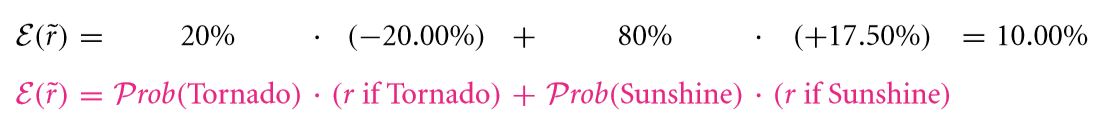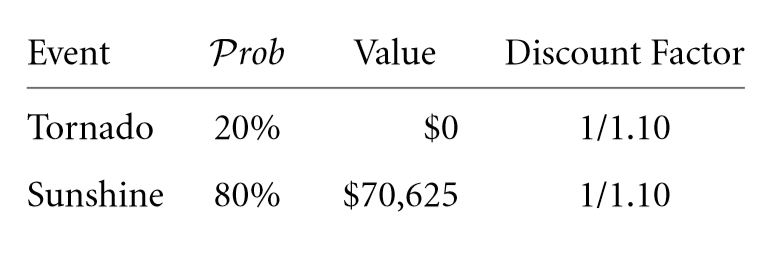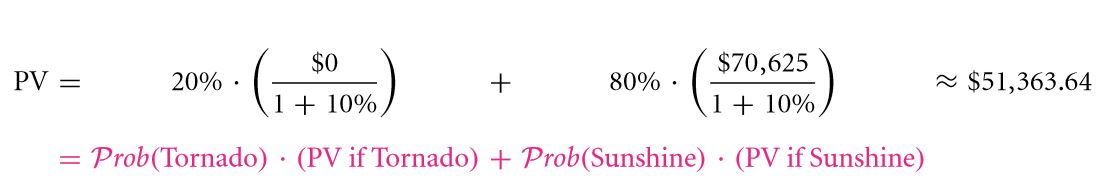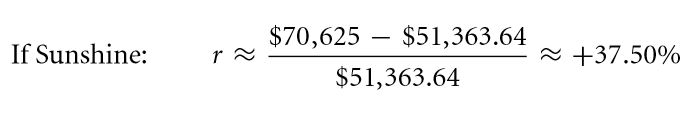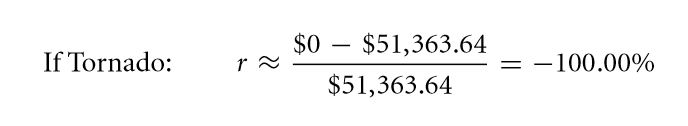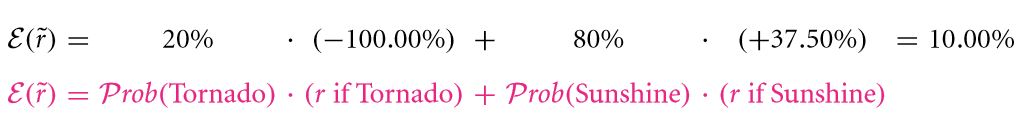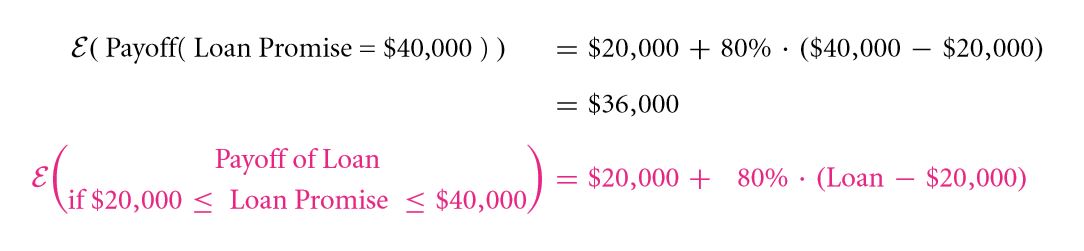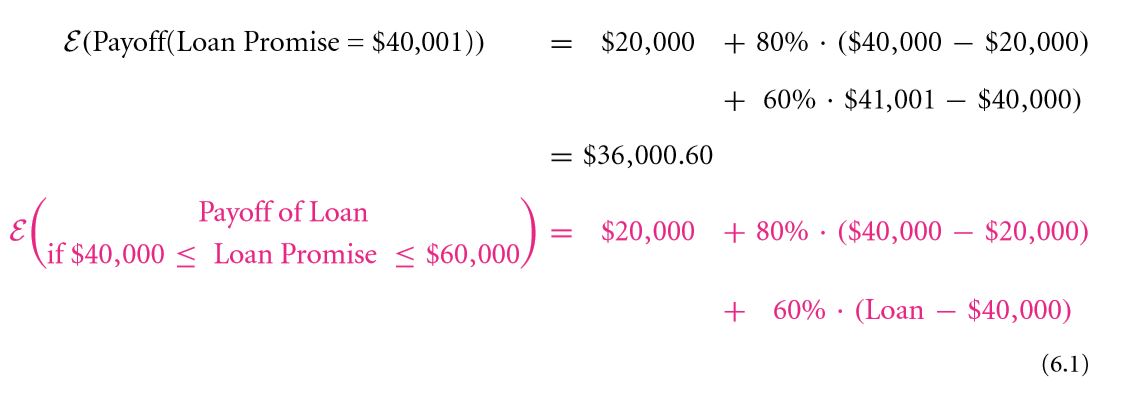Splitting Uncertain Project Payoffs Into Debt and Equity

The major reason behind teaching you the idea of payoffs in depth is the fact that they ought to aid in the understanding of cash flows. Once you are done with the payoff, the next thing that you ought to have a firm idea about in the event that you wish to be successful in the field of finance is the differed between a levered equity or ownership and a debt or a loan. Levered ownership can be considered to be whatever an individual is left with after clearing his or her debt.

If you consider a large number of projects in today’s world, you ought to figure out that most of them are either funded by levered or debt equity. The difference between the various obligations such as tax obligation and a debt ought to be discussed in details under the scope of the next chapter. Another thing that will be discussed in the next chapter is how the idea of equity can be used to replace managers who are not giving the desired level of performance.

That definitely ought to give you a brief idea regarding the difference between an equity and debt. In the event that you mortgage a house, the house is no longer your own until and unless all the debts have been cleared. Individuals may be the levered owner of their very own income as well, in case of student loans. This implies that an individual can cherish his entire salary only after he or she has cleared the loan.

A major question that ought to pop up in the minds of most students is what if the project fails or the career collapses (in case of student loans)? What will the lender and the levered owner receive? Here one needs to approximate the correct compensation value both for the levered owner and the lender.

Calculating the present value of a payoff that depends on various factors has already been discussed. In case of a building collapsing, it has paid off under 2 conditions. Here the building falls under the category of such a claim, i.e. the outcome depends on various adverse conditions including climatic conditions. The value of the various state contingent claims such as equity and debt can be computed with the help of the payoff.

Anecdote

Limited Liability

Several issues arose in the field of finance during the Renaissance. As a result, after its completion, an idea referred to as limited liability was introduced. However, it wasn’t that popular until the 19^th and 20^th century.

“If you consider the discoveries of the modern era, the corporation of limited liability is certainly the greatest. It is even more important than electricity and steam” – this is what the President of Columbia University had to say in 1911. This even allowed the construction of legal houses as a result of which corporations were able to become entities.

6.4 A The Loan

Before moving on with this chapter, there are certain assumptions that needs to be made. Firstly, let us assume at a particular building worth $ 76,363.64 is funded with a mortgage of about $25,000. Under such a circumstance, the project in turn splits itself into two and each half is a separate entity and allows individual ownership. The two separated projects can be classified as follows:

• Residual Building Ownership.
• Mortgage Lending.

The 1^st refers to having a building’s ownership yet under the constant obligation of repaying the mortgage. The investor isn’t going to receive a penny once the debt has been cleared. This forms of residual ownership is often referred to as stock / equity or levered equity to be more precise. Well, the important question now is what should be the interest rate? First let us consider a situation where in the mortgage value is same as above, i.e. $25,000 and the tornado actually strikes which ought to bring down the value of the building to about $ 20,000.

Here the lender might as well seize the property but he or she is certainly not given the authority to lay their hands on anything else that the client possesses. This is what a no – recourse loan looks like. This setup where the liability is limited offer only one option for the creditor and i.e. seizing the property.

If you consider financial securities on a large scale, you ought to figure out that limited liability is predominant. In certain cases in the US, the owner’s liability is not limited. The maximum amount that the owner can lose is what he had initially put in, i.e. the value of the building.

Consider the project “Mortgage Lending”, here we need to calculate its present value with the help of the problem in 6.2 where the credit risk is used to find the desired rate of interest. Make the payoff as follows:

The lender ought to receive the promised amount according to whether the tornado has struck or not. If it has indeed struck, the amount is $20,000. Now in return for lending $25,000 the lender needs to compute what he stands to receive if the tornado doesn’t strike in the following manner:

The promise value is then obtained from this equation in the following manner:

This is the promised amount considering the scenario where in the tornado doesn’t strike. $29,375 is promised as a pay off in the event that the tornado doesn’t strike. The return rate of the creditor ought to be equal to the promised return rate:

This is the minimum interest rate at which the creditor can provide the loan. In the event that the tornado strikes, then the same rate falls down to

Furthermore, the creditors expected return rate is computed by

Hence, 10 % and 17.5 % are the expected and quoted rates of return respectively. The expected rate is common to that of a risk neutral environment.

6.4 B The levered equity

The calculations for computing the current worth of the building to be $ 76,363.64 have been shown earlier. Here we shall figure out the expected rate of return that ought to suffice as far as the owner of a residual building is concerned. It is clear that an individual needs to clear an installment of $ 51,363.64 once he or she has received a loan amount of $ 25,000. As a compensation for the individual lending you $25,000 you must promise to pay him about $ 29,375 the following year. There are two possibilities at this point:

• The tornado doesn’t strike and your building becomes worth $ 70,625, i.e. $ 100,000 – $ 29,375.
• However, in the event that the tornado strikes and you’re building falls apart, the lender ought to seize your entire property and your investment ought to go in vain.

The payoff is given below:

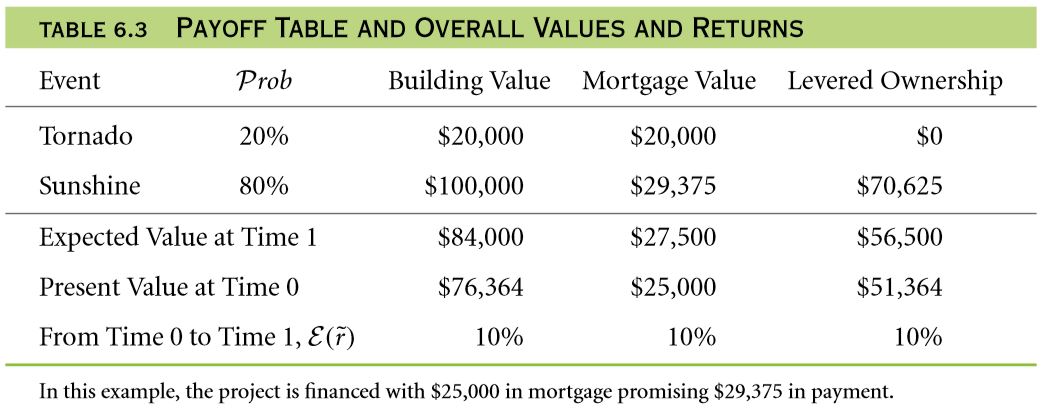
This table is quite useful at the time of computing the expected payoff for the levered building in future is concerned. 1 /5 of $ 0 + 4 /5 of $ 70,625 = $ 56,500. As a result, the current worth of the building can be calculated as follows:

The corresponding return rates are given below in the event that the tornado strikes / doesn’t strike:

The expected return rate is as follows:

6.4 C Reflections on the example: payoff tables

By now, you must have a firm idea regarding pay off table. Now, what if you are asked to define them. Well, these are nothing but fundamental tools that ought to come in handy at the time of considering various financial claims and projects. These tables are extremely sensitive, as shown in the Table 6.3. For project outcomes that are normally distributed, there can very well be an infinite number of states.

This often turns out to be a cumbersome task. However, it is indeed possible for you to estimate the outcomes even when they are complex and continuous. However, the number of discrete outcomes are limited to 10.

Table 6.3 provides us with the expected return rates, present values, pay offs that are state contingent and the various expected payoffs. Irrespective of whether an individual own the levered equity or the mortgage, he or she ought to be at the same position as having the ownership of the entire building. Irrespective of whether an individual falls under the category of a creditor or an unlevered building owner or a levered building owner, he or she falls under the category of claims that are state contingent.

NOTE: In the event that you come across multiple possibilities, the first thing you must do is make the payoff table that contains the probability of occurrence of each event in accordance with the payoff that ought to be a state contingent one.

Exercise
Q 6.15 Given: Mortgage = $ 25,000, Equity = $ 51,364 and PV = $ 76,364. Percentage financed by the mortgage = 32.74 % and the remaining is equity financed. Compare the similarity of this project with the project where two partners are building a house together.

Q 6.16 You may even go for a finance that gives you 80 % of the project amount instead of 32.74 %. Construct the table for this case.

Q 6.17 Considering a situation where in the building being observed is not occupied. The value of the building is the capital amount. However, if you consider a real world scenario, the owners earn quite a bit of money from rent. If the individual renting the houses pays $ 11,000 on an average every year, irrespective of the state, the mortgage repayment may be carried out after the rent has been cleared for a particular year. Consider the resale price of the house to be $ 120,000 in the event that the tornado doesn’t strike and $ 20,000 if it does strike. Take the discount rate to be ten percent.

1. Find the promised interest rate if the lender lends $ 25,000.
2. Find the value of the building in the event that the owner himself or herself resides in the building?
3. Find the current value of ownership of residence.
4. Find the current building value.

6.4 D Reflections on the example: debt and equity risk

So far, the term risk hasn’t been discussed in details. If you consider the world to be uncertain, you don’t need to worry about what you are going to get and its uncertainty. The expected return rate is everything you need to know. However, even in case of a world that is risk neutral, the risk may be assessed. The only thing is that there is no extra premium or compensation as far as the risk is concerned. So, arrange the following types of ownerships on the basis of the risks involved:

• Loan ownership.
• Full ownership.
• Levered ownership.

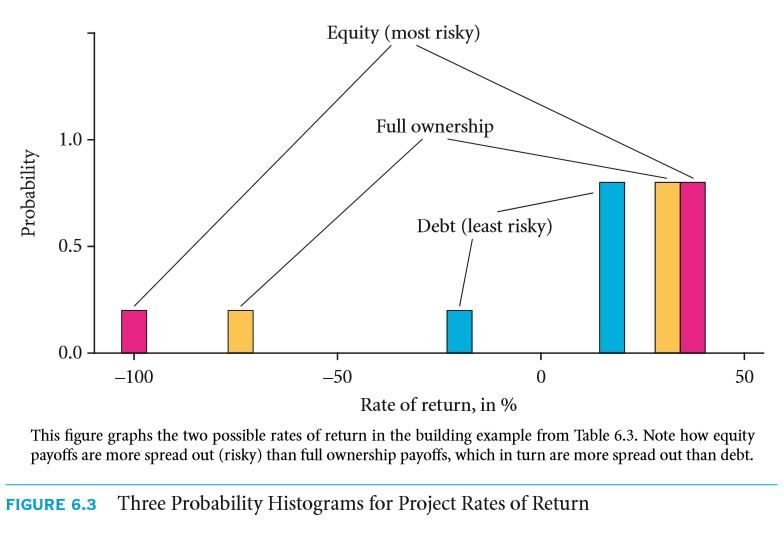
The probability of the equity to earn 37.5 percent and to lose everything is 80 % and 20 % respectively. Consider the return rates in figure 6.3 shown with the help of histograms. As per the graph, the ownerships are listed in ascending order above.

The building gets split into another risky project in the event that the owner seeks for a mortgage. He the mortgage is comparatively less risky than the levered building. Owning the full building on the other hand comes with a considerably average risk. In most of the examples in this chapter, away risk preferences have been taken into consideration which under most circumstances isn’t that useful.

If you consider a real world scenario, every project has a levered owner and a lender. Both the building owners and corporations must have a clear idea as far as the terms equity and debts are concerned. Individuals expect a 10 % return is most projects in the risk neutral world. This is due to the fact that this percentage is considered to be the universal premium (for any sort of further details or queries, go to section 6.2 C).

The risk premium is taken to be zero by assuming a risk neutral world. In such a world, irrespective of the risk, investors are ready to invest as long as they are promised a return rate of 10 %. In case of risk aversion, a lower return rate ought to be expected, i.e. an expected rate of return that is extremely low in comparison to the project value).

The stocks of a particular company are nothing but levered ownership. Under such an ownership, the owner ought to get the promised amount only after the liabilities have been dissolved. Whatever you have done so far are extremely important in the event that an individual wants to work with claims that are state contingent such as equity, debt, etc.

The idea of calculating the contingent state has been clearly explained with the help of the building example. All the parameters discussed in this chapter ought to be calculated. On the introduction of risk aversion, the only alteration will be in the number of basis points. These points are mostly required for risk compensation. Debt is the safest claim, project is the claim with medium risk and equity is perhaps the richest claim.

Exercise

Q 6.18 It may so happen that the loan promises a return of $25,000 but doesn’t provide the same.

1. What do you actually get?
2. Compare the risk factor of the Levered Building Ownership and the Full Building Ownership.
3. Find the promised return rate.
4. Re – compute the table.

Q 6.19 Considering that the payoff is $20,000, repeat the experiment. Compare the risk factor of the Levered Building Ownership and the Full Building Ownership for a risk free project.

6.4 E What “leverage” really means—financial and operational leverage

Another common term in the field of finance is leverage which is often used synonymous with debt. You have already come across the term levered equity. If you consider the term lever, it is a simple machine whose sole purpose is amplification of the input to produce the desired output. In terms of finance, it is a small equity that is capable of running a firm and is aware of the firm’s net loss or gain.

This means that a small investment or a change may result into a large outcome. This has been clearly stated in the building example as well as in FIGURE 6.3. Debt in the field of finance is often considered to be a lever. However, there are several other leverages in the field that are computed using the various liabilities such as obligations on pension, account payable, etc. The concept isn’t limited to the finance market, it is a general term. It should be considered from a macro level.

Thanks to the idea of leverage, an individual is able to take control of a house that costs $ 76,364 at $ 51,364. Well, it doesn’t end there. Considering that there is no tornado, you ought to receive a return of 37.5 % instead of 30.95 %. On the other hand, if by chance the tornado strikes, you lose everything. Hence, you can now understand the use of leverage in finance, i.e. amplifying the stake.

The idea goes by the saying that a small force (investment in this case) can be used to do the work of a much larger force. To take a look at the various types of levers, it is recommended for you to go through Table 6.4. This table shows that one may receive an outcome of $ 1000 or $ 200 from an investment of $ 475 on a machine.

In addition to this, the machine offers a resale value of $ 150. The leverage is also capable of magnifying the return by -1 or + 5.4. Leasing the machine is perhaps another suitable option here. If the conditions are favorable one may earn up to 1.42 times. However, under unfavorable circumstances the same person may lose .26 times the amount.

Another thing that the individual can do is pay $ 75 as labor cost instead of $ 250. This increases the risk factor by – 38 % but at the same time by + 208 % in case of no leverage. For alternatives examples on production, take the final example into account.

6.4 F Working with more than two possible outcomes

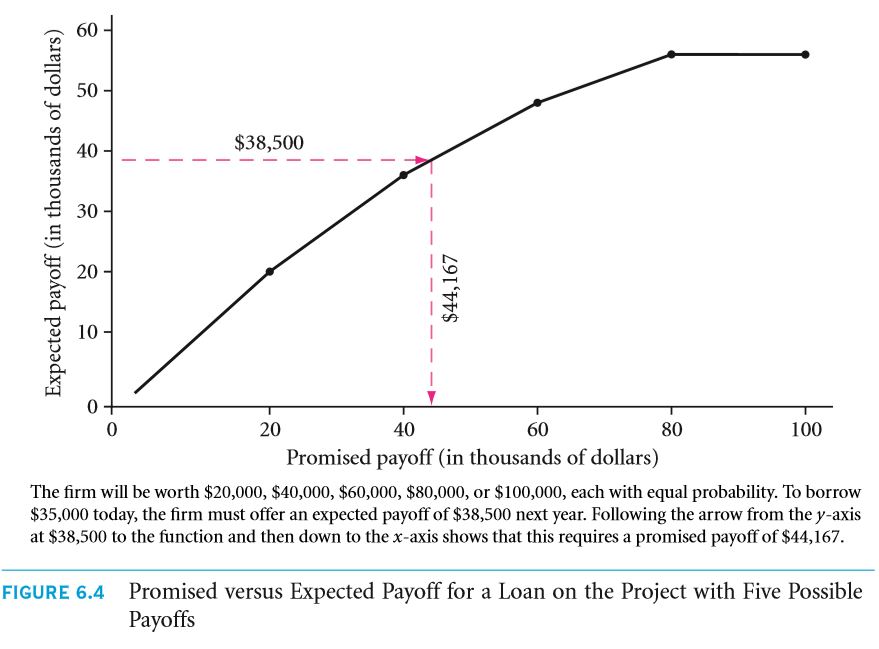
As the heading suggests, this section will be teaching you how to work with a project that has more than 2 possible outcomes. You may come across a situation where the building may be worth $ 100,000 or $ 80,000 or $ 60,000 or $ 40,000 or $ 20,000, each having the same probability of occurrence. In addition to this, the expected rate of interest is taken as 10 %.

            Let PV = $ 60,000 / 1.1 = $ 54,545.45 for a loan with a promised return of $ 20,000.

Under such a situation, the lender will definitely expect $ 20,000.

In the event that the promised return for a particular loan is $20,001, the individual will definitely not be satisfied with anything less than that. He or she will also be expecting the marginal value as well with a probability of 4 / 5. For a promised amount of $ 40,000, the expected return value is:

What will an individual expect to receive in the event that the loan promised $40,001 ($ 20,000 as fixed return with a probability of 1, the next $ 20,000 with a probability of 4 / 5 and the marginal value, i.e. the one dollar with a probability of 3 / 5.

The payoffs that are expected have been plotted against the promised payoffs in the Figure 6.4. Computing the value of a mortgage becomes all the more easier with the aid of this graph. Suppose you lend $ 35,000 to a person, what should be the promised amount? Well, it can be calculated as follows:

• . $ 35,000 which is equivalent to $ 38,500. On the other hand, if $ 38,500 is the expected payoff, the promised amount is $ 44,000 approximately. $ 44,167 is approximated to $ 44,000. The maximum amount that can be borrowed is $ 55,000.

Links of Previous Main Topic:-

• Introduction of corporate finance
• The time value of money and net present value
• Stock and bond valuation annuities and perpetuities
• A first encounter with capital budgeting rules
• Working with time varying rates of return
• Uncertainty default and risk
• Interest rates and credit risk default risk

Links of Next Financial Accounting Topics:-

• Exercise
• Corporate governance
• International finance
• Options and risk management