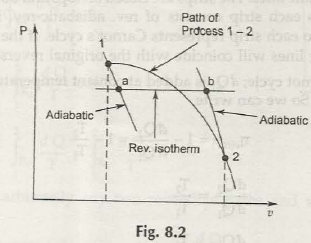
First consider this following figure:
The points that are vital here are that:
- There are going to be two reversible adiabatic paths namely, 1 – a and b – 2.
- The isothermal path a – b is going to be drawn in such a way that conditions of 1 – a, b – 2 and 1 – 2 are going to be same.
Now after we apply rules found from 1st law upon 1 – 2:
Q1-2 = U2 –U1 + W1-2
for process (1 -a – b – 2)
Ql-a-b-2 = u2– u1 + wl-n-b-2
wl-2= wl-a-b-2, we can write
Ql-2 = Ql-a-b-2
= Q1-a + On-b + Qb-2 =0+Qa-b+ 0
Or Ql-2 = Oa-b
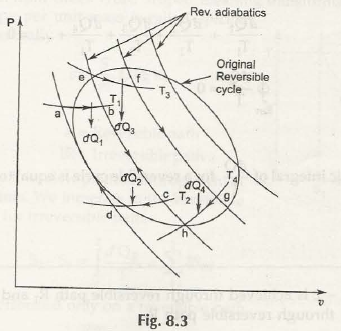
For the next step we will consider the figure below:
Here, the proven factor is that heat transferred from 1 – 2 and a – b are equal.
Points out of this figure:
- If there is going to be same end cycle then you can replace any type of reversible paths with zigzag paths.
- In the zigzag reversible path, there are going to be one adiabatic, one isothermal and again one adiabatic path step by step. This is the way the complete cycle of reversible path can be completed with a zigzag path.
- Here the heat transferred from the isothermal process is going to be equal as in the original one.
- In the figure above you will find an original reversible cycle which is divided into strips of number of reversible adiabatic lines.
- All strips have both top and bottom ends for a reversible isotherms.
- You are going to finds strips such as, rev. adiabatic-rev. isothermal-rev. adiabatic-rev. isothermal etc.
- If you find many strips and large in volume then the zigzag path will actually present an original view of reversible path.
- All the strips will provide Carnot’s cycle.
Now consider the following equations:
Carnot cycle; aQ1 is added at contact temperature T1 and aQ2 is rejected at temperature T2. So we can write
ɳ c(rev) = 1 – dQ2 / dQ1 = 1 – T2 / T1
dQ2 / dQ1
dQ2 / dQ1
dQ2 /T1 = – dQ1/ T2 , He have dQl is positive and d”Q2 is negative
thusdQ2 /T1 = – dQ1/ T2 (taking proper sign of heat)
dQ2 /T1 + dQ1/ T2 =0
Similarly for the elemental Carnot cycle we have
dQ3/T3 = – Dq4/ T4 =0
Thus applying the above procedure for all the elemental Carnot’s cycles, we get theequation for whole original cycle.
Thus dQ2 /T1 + dQ1/ T2 + … = 0
Or ʠREVdQ/T = 0
The cyclic integral of dQ for a reversible cycle is equal to zero. This is the Clausius theorem.
Links of Previous Main Topic:-
- Open system and control volume
- Conversion of work into heat
- Introduction to carnot cycle
- Clausius inequality entropy and irreversibility introduction
- Reversible adiabatic paths do not intersect
- Clausius theorem
Links of Next Mechanical Engineering Topics:-
- Entropy
- Entropy temperature plot
- Clausiuss inequality
- Entropy change in an irreversible process
- Principle of increase of entropy
- The degree of irreversibility of and irreversible process
- Summary of first and second law by clausius
- Practical use of entropy principle
- First law and second law combined
- Analysis of thermodynamic equations
- Ideal gas or perfect gas
- Introduction about air standard cycles
- Properties of pure substances introduction
- Vapour compression refrigeration cycle introduction
- Basic fluid mechanics and properties of fluids introduction