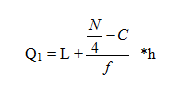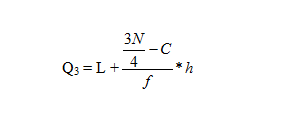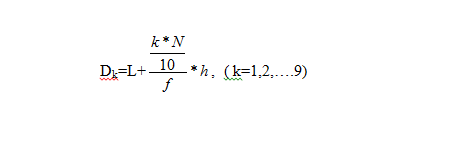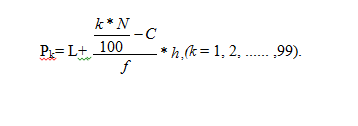In a data set the median is the middle part of it. It means it divides the data in two different parts. But, quartiles divide an array or data set in four parts. If you go with Dectiles, then division of arrays takes place in ten parts. This clears that percentiles which means hundred divides an array into hundred parts.
In quartiles as the array divides into four parts so, the second part of that array will always be the value of the Median.
For the lower quartile or the first quartile the formula is used as
For the above formula
L is the lower limit of Q1
f is the frequency of that class
h is the width of that class
C is the cumulative frequency
With the above formula you can also find out the 3rd quartile as
In the same way the Dectiles can be obtained with
So, it is very simple for anyone observing each Dectile. The upper limit is always 9. For a percentile the formula needs to be used is–
The upper limit for percentile is always 99.
Now, anyone can get the difference of quartiles, Dectiles and percentiles. However, for each section the value gets changed according to the particular class. So, For the Dk class containing Dectile the cumulative frequency > (k*N) /4.
In the same way for Pk the cumulative frequency > (k*N) /100.
With the proper knowledge of this the student or the observer can easily find out the particular data or record related to a specific statistical array.
Example 6. Determine (a) Q1, (b) Q3 , (c) D5 (d) P80 from the following distribution :
Links of Previous Main Topic:-
- Introduction to statistics
- Knowledge of central tendency or location
- Know about arithmetic mean
- Explanation of geometric mean
- The proper explanation of harmonic mean
- Acquire the suitable knowledge of median
- Know the exact meaning of mode
Links of Next Statistics Topics:-
- Definition of dispersion
- Moments
- Bivariate distribution
- Theorem of total probability addition theorem
- Random variable
- Binomial distribution
- What is sampling
- Estimation
- Statistical hypothesis and related terms
- Analysis of variance introduction
- Definition of stochastic process
- Introduction operations research
- Introduction and mathematical formulation in transportation problems
- Introduction and mathematical formulation
- Queuing theory introduction
- Inventory control introduction
- Simulation introduction
- Time calculations in network
- Introduction of game theory