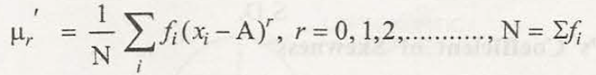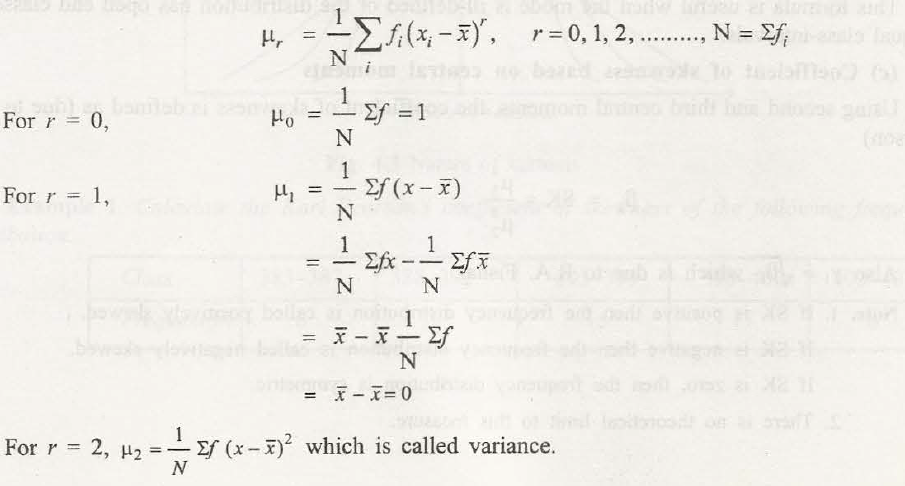The term moment when it comes to statistics can be used in relation to analogous to moments of force. In case of statistics, moments come with constant values that are available in given distribution which can enable to understand nature and form of distribution.
The moments taken from mean are referred by µ. You will get to know that the first four moments are very important which can describe different types of statistical distribution. The formula for first four moments is:
The first moment about the mean, m1 =
The 2nd moment about the mean, m2 =
The 3rd moment about the mean, m3 =
The 4th moment about the mean, m4 =
Where,
X = the mid-value of the class
=the mean
f = the class frequency and
N = the total frequency.
Moments that come in mathematical statistics may include basic calculation. Such calculations can also be used to find out probability distribution’s mean, variance and skewness.
First moment
For first moment we set s=1. The formula is said to be:
(x1x2 + x3 + . . . + xn)/n
This can be an identical formula for sample mean.
Second moment
The formula for 2nd moment is:
(x12 + x22 + x32 + . . . + xn2)/n
Third moment
The formula is:
(x13 + x23 + x33 + . . . + xn3)/n
Links of Previous Main Topic:-
Links of Next Statistics Topics:-
- Bivariate distribution
- Theorem of total probability addition theorem
- Random variable
- Binomial distribution
- What is sampling
- Estimation
- Statistical hypothesis and related terms
- Analysis of variance introduction
- Definition of stochastic process
- Introduction operations research
- Introduction and mathematical formulation in transportation problems
- Introduction and mathematical formulation
- Queuing theory introduction
- Inventory control introduction
- Simulation introduction
- Time calculations in network
- Introduction of game theory