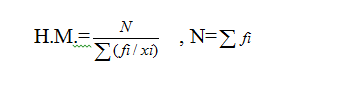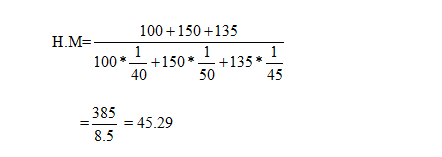The Harmonic mean is an important part of statistics as it comes under central tendency. Arithmetic mean and harmonic mean are completely different.
In simpler form the harmonic mean can be deducted or defined as the reciprocal of addition of numbers in a set and the value of the sum gets divided by N. For example the H. M. of 2 different numbers 4 and 9 can be found out by 2/(1/4 +1/9) = 2/(13/36) = 72/13. Simple way can help in more than 2 numbers also.
However, in the case of a frequency distribution in the group, the determination can be done in a different way. It means H.M. = N/∑ ( fi/xi)
Here, N means ∑ fi. In addition xi is considered as class mark.
So, a grouped frequency means the two different values suppose the distance and speed of a vehicle. In this, H.M. can be determined by adding of reciprocal of speed multiplied by its related distance and the value of that addition gets divided by N which is the total distance.
With the proper examples and by solving different questions anyone can easily notice that how all three parts of Mean i.e. A.M., G.M. and H.M. are different than each other.
Link of Previous Main Topic:-
Links of Next Statistics Topics:-
- Definition of dispersion
- Moments
- Bivariate distribution
- Theorem of total probability addition theorem
- Random variable
- Binomial distribution
- What is sampling
- Estimation
- Statistical hypothesis and related terms
- Analysis of variance introduction
- Definition of stochastic process
- Introduction operations research
- Introduction and mathematical formulation in transportation problems
- Introduction and mathematical formulation
- Queuing theory introduction
- Inventory control introduction
- Simulation introduction
- Time calculations in network
- Introduction of game theory