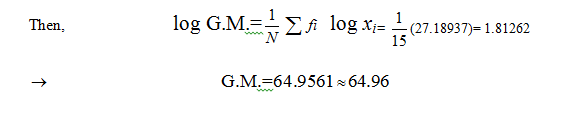The Geometric mean is defined as the central tendency of numbers in which the mean is derived through the product of the numbers. Thus, it is not alike as Arithmetic mean value as in arithmetic mean the sum of the products is important.
For finding out the simple frequency geometric mean, data for x1, x2 up to xn is defined as
Sometimes the grouped frequency is considered in the form
Class mark is taken as x1, x2 and N is considered as the summation of frequencies. Log x needs to find out in the first step for group frequency and then it needs to be multiplied with f or the frequency value. And the total of f log x can easily be divided by the total frequency value of N. The N can easily be explained as the total addition of frequency.
Now, it is clear that how to find out geometric mean in statistical data.
Links of Previous Main Topic:-
Links of Next Statistics Topics:-
- Definition of dispersion
- Moments
- Bivariate distribution
- Theorem of total probability addition theorem
- Random variable
- Binomial distribution
- What is sampling
- Estimation
- Statistical hypothesis and related terms
- Analysis of variance introduction
- Definition of stochastic process
- Introduction operations research
- Introduction and mathematical formulation in transportation problems
- Introduction and mathematical formulation
- Queuing theory introduction
- Inventory control introduction
- Simulation introduction
- Time calculations in network
- Introduction of game theory