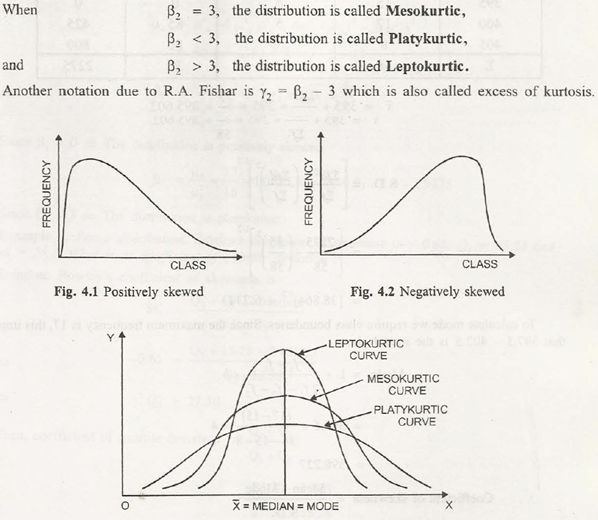
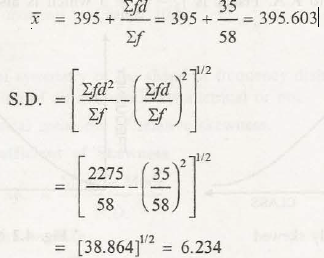Distribution of data as well as probability distributions does not come in same shape. There are some that are found to be asymmetric and also skewed to left or right. There are also other distributions which are bimodal and support two peaks. The other feature that needs to consider while discussing about distribution is shape of its tails of distribution that is identified far left and far right.
Kurtosis can be adapted to measure thickness and heaviness of tails of distribution. In case of kurtosis of a distribution, you can classify them into three main categories:
- Mesokurtic
- Leptokurtic
- Platykurtic
Kurtosis is further defined as:
Where,
n is represented as sample size
Xi is the ith X value
X the average
S is sample standard deviation
The exponent is known to be the summation and it is “4”. Kurtosis is actually referred as “4th standardized central moment for probability model.”
Kurtosis is often confused with measurement of peakedness of distribution. It is a measure that can easily define shape of distribution’s tails in regard to overall shape.
Links of Previous Main Topic:-
- Introduction to statistics
- Knowledge of central tendency or location
- Definition of dispersion
- Moments
- Skewness
Links of Next Statistics Topics:-
- Bivariate distribution
- Theorem of total probability addition theorem
- Random variable
- Binomial distribution
- What is sampling
- Estimation
- Statistical hypothesis and related terms
- Analysis of variance introduction
- Definition of stochastic process
- Introduction operations research
- Introduction and mathematical formulation in transportation problems
- Introduction and mathematical formulation
- Queuing theory introduction
- Inventory control introduction
- Simulation introduction
- Time calculations in network
- Introduction of game theory