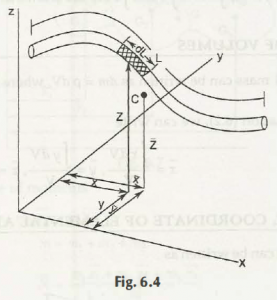
Suppose the value of moment of area is zero about any point in the given plane. The point at which the value becomes zero, it is called centroid of that area.
For the determination of centroid of any given figure, we should use the above technique. Whether we have to determine centroid of line or centroid of volume, it can be found conveniently.
In other words, centroid is the geometric center of any plane figure about an axis. For an object in n-dimensional space, the centroid is the value of mean position of all points. In this aspect, the centroid of straight line of length L about a reference axis can be rested at the position of half of its length or L/2.
Locating of Centroid
Centroid can be located by using two different methods for different figures- those are Plumb Line Method and Balancing Method.
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Center of gravity and center of mass
Links of Next Mechanical Engineering Topics:-
- Centroids of areas
- Centroids of volumes
- Centroidal coordinate of elemental area
- Centroidal coordinate of elemental volume
- Coordinates of centre of mass of composite bodies and figures
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction