Center of Gravity and Center of Mass

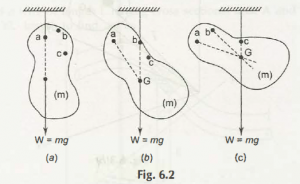
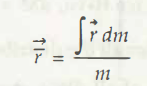With reference to figure 6.2 the body of mass is stopped by the cord which are not extended from point a. The W is denoted by W = mg which will act on vertical basis moving downward. A dotted line is drawn by us from point a moving downwards, and then the body is separated from the point c respectively. All the lines which are drawn vertically meet at one fixed point in above figure b and c at point G which is called Center of Gravity.

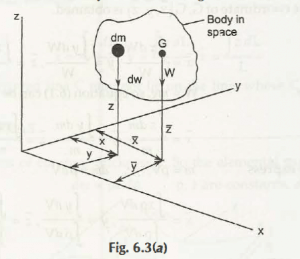
 In order to calculate center of gravity in mathematical term we should move for fig 6.3 a and b

By moving downward side, in order to find dW in y axis we will see

dM = x dW

Or it can be taken as  M = ʃ x dW for all other distributed forces

 In order to get the result about W which lies in y axis we will come across with

M1  =xW

According toVarignon’s theorem (Principle of moments) we can write

M1 =M

x W = ʃ x dW

= x dW / W

Same as we can also write the expression for y and z as follows

Y = ʃ y dW /W , z =  ʃ z dW /W

Thus, the coordinate of G, G (x, y,z) is obtained.

x = ʃ x dW /W , y = ʃ y dW /W ,z = ʃ z dW/W

We have

W = mg, so equation (6.1) can be rewritten as

x = ʃ x dm /m , y = ʃ y dm /m ,z = ʃ z dm/m

Now we express

m= Pv ,           dm = pdV

x = ʃ xpdV / ʃ p dV,  y = ʃ y dV / ʃ p dV , z = ʃ z dV / ʃ p dV

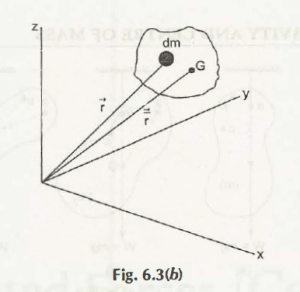
Equation (6.2) may be described in vector form (Refer Fig. 6.3(b))

Equations (6.2), (6.3) and (6.4) have no reference about ‘g’ (gravitational effect). Therefore, we can come across with unique point (X, y, Z) which is called as the centre of mass. The centre of mass interlinked with the centre of gravity as long as g remain constant.

Links of Previous Main Topic:-

• Introduction to statics
• Introduction to vector algebra
• Introduction concept of equilibrium of rigid body
• Friction introduction
• Introduction about distributed forces
• Center of gravity and center of mass

Links of Next Mechanical Engineering Topics:-

• Centeriods of lines
• Centroids of areas
• Centroids of volumes
• Centroidal coordinate of elemental area
• Centroidal coordinate of elemental volume
• Coordinates of centre of mass of composite bodies and figures
• Area moments of inertia in rectangular and polar coordinates
• Mass moment of inertia introduction
• Work done by force
• Kinematics of particles
• Position vector velocity and acceleration
• Plane kinematics of rigid bodies introduction