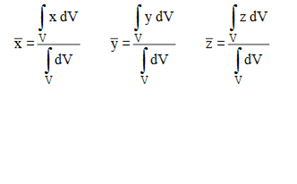Centroid of volumes can be determined similar to the centroid of lines. Suppose the value of moment is zero at a point, it is the centroidal point of that figure.
For this condition, the value of distance of the point from the axes in three dimensions is considered for determining the integral. The choice of one, two or three integral formulation is used depending upon the differential volume of the figure.
Suppose the elementary mass and volume be dm and dV then the equations of integral can be given by –
For three-dimensional figure, the ratio of integrals are written in the following manner-
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Center of gravity and center of mass
Links of Next Mechanical Engineering Topics:-
- Centroidal coordinate of elemental area
- Centroidal coordinate of elemental volume
- Coordinates of centre of mass of composite bodies and figures
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction