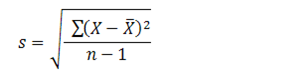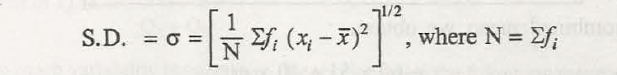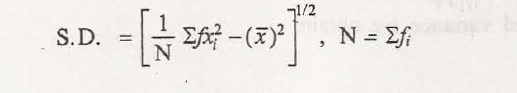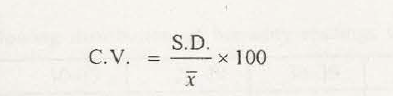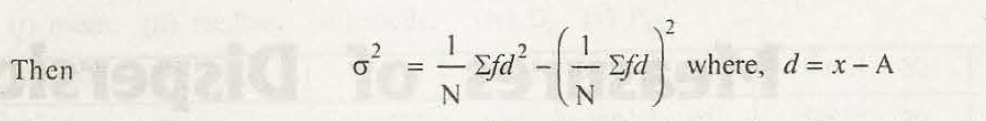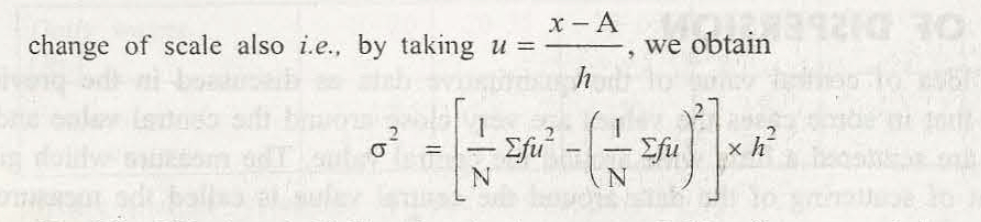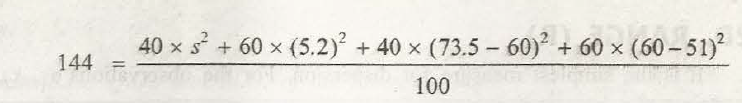Standard deviation is known to be a measure that occurs around spread of scores which happens within set of data. Usually, while adopting standard deviation, we prefer to calculation SD of a population. It is presented along with data adopted from sample which can enable to estimate population of standard deviation from sample standard deviation.
The two standard deviations:
- Sample SD
- Population SD, can be calculated differently
The formula of standard deviation (SD) is
S= sample standard deviation
Σ= sum of
n= number of scores in sample
Though this formula may appear to be a bit confusing, but you can break down and simplify it. You can understand step-by-step interactive process through example.
Step 1: Find out the mean
Step 2: Find out square of distance to mean for every data point
Step 3: Sum of the values gained from Step 2
Step 4: Divide it by number of data points
Step 5: Take up square root
While calculating standard deviation of sample you will identify that it comes with a slightly different formula:
s = √ [ Σ ( xi – x )2 / ( n – 1 ) ]
S is represented as sample standard deviation
X is sample mean
Xi is ith element from sample
n is number of elements found in sample
Standard deviation is equal to that of square root of variance.
While calculating the variance of any data set it is possible through taking arithmetic mean of squared difference between different value and mean value. Squaring different comes with three advantages:
- Squaring makes each and every term very position so this means that value above mean would not have cancel values below mean
- Squaring may add up more weight to larger differences and in some cases, there is an extra weight which is appropriate from mean that is highly significant
- Mathematics may appear to be highly manageable while using this to measure subsequent statistical calculations
Links of Previous Main Topic:-
Links of Next Statistics Topics:-
- Moments
- Bivariate distribution
- Theorem of total probability addition theorem
- Random variable
- Binomial distribution
- What is sampling
- Estimation
- Statistical hypothesis and related terms
- Analysis of variance introduction
- Definition of stochastic process
- Introduction operations research
- Introduction and mathematical formulation in transportation problems
- Introduction and mathematical formulation
- Queuing theory introduction
- Inventory control introduction
- Simulation introduction
- Time calculations in network
- Introduction of game theory