Resolution of Force:

Forces can be resolved into two componentsi.e., horizontal component of force and vertical component of force. It is called resolution of a force.

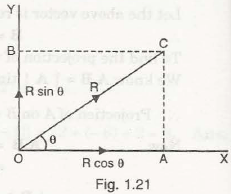
Let us consider a force R is making an angle  with the horizontal as shown in Fig. 1.21

The horizontal component of R = R cos θ            (Along x-axis)

The vertical component of R = R sin θ            (Along y-axis)

The above components show the resolution of force F along x and y direction.

Resolution of Number of Coplanar Forces:

Forces acting in one plane are termed as coplanar forces and these forces run parallel to the plane.

Let us consider three forces R1, R2 and R3acting on a single plane making angles θ1, θ2 and θ3 respectively as shown in Fig. 1.22

Resultant of all three forces be R

Horizontal resultant component be H

Vertical resultant component be V

Angle with the horizontal axis be θ

Then,

Horizontal component of force R1 = R1 cosθ1

Vertical component of force R1 = R1 sinθ1

Similarly,

Horizontal component of force R2 = R2 cosθ2

Vertical component of force R2 = R2 sinθ2

And,

Horizontal component of force R3 = R3 cosθ3

Vertical component of force R3 = R3 sinθ3

Thus,

Horizontal resultant component = Sum of all the forces in the plane along x-axis

H = R1 cosθ1 + R2 cosθ2 + R3 cosθ3+………..

And,

Vertical resultant component = Sum of all the forces in the plane along y-axis

V = R1 sinθ1 + R2 sinθ2 + R3 sinθ3 +………..

To determine the angle between resultant force and horizontal axis,

tan θ=V/H

Composition of Forces:

For the above determination, we can say the composition or resultant of forces is the overall value of all forces acting on the body. The resultant of forces will act as per the value of angle between the resultant of force and the horizontal axis in the same plane of the forces.

Moment of Force:

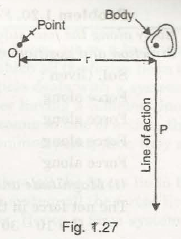
Moment of force can be calculated by multiplying the force and perpendicular distance from the point of its line of action.

Let us consider a body of mass M is exerted by a force P as shown in Fig. 1.27

Perpendicular distance of the line of action of the force from point O be r

Then,

Moment of force can be given by-

= P x r                          (About point O)

Note:

• The line of action of force is in downward direction. It means the force can rotate the given body in clockwise direction about point O. It is called clockwise moment of force.
• In case, the line of action of force tends to rotate the body in anticlockwise direction, it is called anticlockwise moment of force.
• In S.I. system, the unit of moment of force is Newton-meter (N-m) and in M.K.S. system, the unit of moment of force is kgf.

For equilibrium condition:

Whenever a force acts on the body, it tends to produce linear displacement of the body. If a moment acts on the body, it tends to produce angular displacement of the body.

If a number of forces act on the body, then the effect of these coplanar forces acted on the body can be equilibrium under specific conditions-

• When the resultant of all forces becomes zero, the body is said to be in equilibrium. In this case, the resultant components i.e. along x-axis, y-axis and z-axis should be zero.
• For equilibrium condition, clockwise moment of force acted on the body should be equal to the anticlockwise moment of force.
• Resultant moment of forces in the place of force about any point should be zero.

For non-equilibrium condition:

Suppose the resultant component of forces in the plane along any given direction is zero but its net moment of forces is not zero. In such cases, the body is not said to be in equilibrium and it is possible to rotate about the given point.

Links of Previous Main Topic:-

• Fluid statics introduction
• Manometers measurement pressure
• Fluid kinematics
• Bernoullis equation
• Basics and statics of particles introduction
• Units and dimensions
• Laws of mechanics in basics and statics of particles
• Lamis theorem in basics and statics of particles
• Parallelogram and triangular law of forces
• Vectors
• Resolution and composition of a force
• Coplanar forces

Links of Next Mechanical Engineering Topics:-

• Resultant of coplanar forces
• Equilibrium of a particle
• Equilibrium of a rigid body
• Forces in space
• Equilibrium of a particle in space
• Equivalent system of forces
• Principle of transmissibility
• Single equivalent force
• Highlights of basics and statics of particles
• Equilibrium of rigid bodies introduction