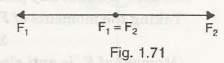Equilibrium of a Rigid Body

If external forces may be parallel or concurrent act on any stationary rigid body, it tends to move or start rotating the body about a particular point in the plane. When the body does not move or rotate about any point, it is said that rigid body is in equilibrium condition.

In other words, when all coplanar external forces are in equilibrium, the summation of these forces and its moment are equal to zero. This is also called the Principle of Equilibrium.

Mathematically,

∑▒〖F=0〗

And,

∑▒〖M=0〗

Where,

F = Coplanar forces

M= Moments

Let us consider the forces be resolved into its horizontal and vertical components.

Hence, it can be written as-

∑▒〖F_x=0〗 and ∑▒〖F_y=0〗

Where,

∑▒〖F_x=〗Algebraic summation of forces along x-direction

∑▒〖F_y=〗Algebraic summation of forces along y-direction

For Non-Concurrent Force System:

The equation of equilibrium can be defined by-

∑▒〖F_x=0〗

∑▒〖F_y=0〗

And,

∑▒〖M=0〗

For Concurrent Force System (when all forcesmeet at a single point):

To get the equation of equilibrium, the moment of forces becomes redundant. So, the equation of equilibrium can be given by-

∑▒〖F_x=0〗

And,

∑▒〖F_y=0〗

Note:

The above equations are considered as the force law of equilibrium. It can be applied for different force systems-

1. Two Force System:

When two equal, opposite and collinear forces act on the system, it is called two force systems as shown in Fig. 1.71

 

 

Here,

F₁ and F₂ are two forces in opposite direction

Let us consider two forces F₁ and F₂ act in opposite direction; have equal magnitudes but both are parallel as shown in below figure.

 

 

From the force law of equilibrium, we get-

∑▒〖F_x=0〗            (No horizontal forces)    ——————————— (1)

And,

∑▒〖F_y=0〗            (F1 = F2)        ——————————— (2)

Now,

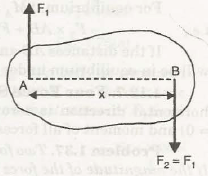
Taking moment at point A can be given by-

MA = – F2 x AB                        ——————————— (3)

Note:

Equation (1) and (2) satisfies the force law of equilibrium but equation (3) does not satisfy. It shows that two parallel, equal and opposite forces can produce a couple.

1. Three Force System:
   

• • Let us consider three force system act on a body so that the body remains in equilibrium as shown in Fig. 1.72,

 

 

Here,

F₁, F₂ and F₃ are three forces acted in different directions from point O

Suppose these three forces are concurrent such that the resultant, R can be given by the line opposite to the force F₃. This resultant force is called equilibrant.

• If all three forces act in the same direction, the resultant force can be given by their summation. Thus, the body tends to rotate or move from its usual position.

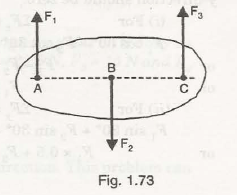
• • When three forces act in the rigid body such that the value of resultant becomes zero. The rigid body is said to be in equilibrium condition as shown in Fig. 1.73

 

 

F₁ be first force act in upward direction at point A

F₂ be second force act in downward direction at point B

F₃ be third force act in upward direction at point C

Then,

From the condition of equilibrium,

∑▒〖F_x=0〗            (No horizontal forces)

And,

∑▒〖F_y=0〗            (F1+ F3= F2)

Now,

Taking moment at point A can be given by-

MA = – F2 x AB    + F3 x AC

Or,

0 = – F2 x AB+ F3 x AC

Note:

It shows that if the value of AB and AC satisfy the above equation, then the rigid body is said to be in equilibrium.

1. Four Force System:

Suppose four force system acts on a rigid body such that resultant horizontal and vertical forces are zero and moment about any point is also zero. The rigid body will be in equilibrium condition i.e,

∑▒〖F_x=0〗

∑▒〖F_y=0〗

And,

∑▒〖M=0〗

Problems on Force System:

Example No 1:

Two forces act on a body with the magnitude of 100 N (for first force) in horizontal direction as shown in Fig. 1.74. Determine the magnitude of second force.

 

 

Given Data:

F₁ = 100 N

F₂= ?

We know that,

For two force system, the magnitude of both forces will be equal, collinear but in opposite direction.

Hence,

Second force, F₂ = 100 N

Example No 2

Three forces act on a body to keep it in equilibrium. If the magnitude of downward force is 400 N, what will be the magnitude of rest two forces?

Solution:

 

 

The above figure shows

F₁ and F₂ are two forces making an angle 30⁰ with the horizontal.

From the force law of equilibrium,

∑▒〖F_x=0〗

The components of force can be given by-

F1cos300 – F2cos300 = 0

Or,

F1–F2= 0

Or,

F1 =F2

∑▒〖F_y=0〗

F1sin300 +F2sin300– 400 = 0

F1x 0.5 + F2x 0.5 – 400 = 0

So,

The value of force F1 can be given by,

2F1 = 400/ 0.5

Hence,

F1 =F2= 400 N

2F₁ = 400/ 0.5

Hence,

F₁ =F₂= 400 N

Alternative Method:

We can also find the values of three force system using Lame’s Theorem.

From the above figure, we can write-

F_1/sin⁡〖〖120〗^0 〗 = F_2/sin⁡〖〖120〗^0 〗  =  400/sin⁡〖〖120〗^0 〗

Or,

F_1/sin⁡〖〖120〗^0 〗   =  400/sin⁡〖〖120〗^0 〗

Or,

F1 =400 N =F2

 

Links of Previous Main Topic:-

• Fluid statics introduction
• Manometers measurement pressure
• Fluid kinematics
• Bernoullis equation
• Basics and statics of particles introduction
• Units and dimensions
• Laws of mechanics in basics and statics of particles
• Lamis theorem in basics and statics of particles
• Parallelogram and triangular law of forces
• Vectors
• Resolution and composition of a force
• Coplanar forces

Links of Next Mechanical Engineering Topics:-

• Forces in space
• Equilibrium of a particle in space
• Equivalent system of forces
• Principle of transmissibility
• Single equivalent force
• Highlights of basics and statics of particles
• Equilibrium of rigid bodies introduction