Forces in space are represented in three dimensions. Each of the forces will be represented with its directional vector.

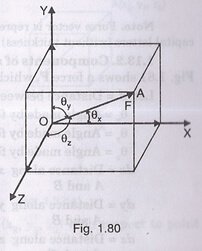
Let us consider force F has its origin from point O as shown in Fig. 180,

Vector OA represents force F

Draw parallel lines to coordinate planes from point A such that it forms a cuboid

Fx be the force component ofxy plane

Fy be the force component ofyz plane

Fz be the force component ofzx plane

θx be angle with x-axis

θy be angle with y-axis

θzbe angle with z-axis

Thus,

Force component can be written in terms of force F as-

Fx= F cosθx

Fy = F cosθy

Fz = F cosθz

Now,

Taking the cosines of the above figure, we get-

l = cosθx

m = cosθy

n =cosθz

According to the cosine law,

cos2θx + cos2θy + cos2θz = 1

or,

l2 + m2+ n2= 1

Now,

Magnitude of force F can be given by considering the direction of forces.

i ̂be the unit vector in x-direction

j ̂be the unit vector in y-direction

k ̂be the unit vector in z-direction

Then,

F = Fxi ̂+ Fyj ̂+ Fzk ̂                ————————- (1)

Or,

|F| = √(Fx2+ Fy2 + Fz2)

Substituting the values of components of force, we get the equation (1) as-

F = F cosθxi ̂+ F cosθyj ̂+ F cosθzk ̂

Components of force:

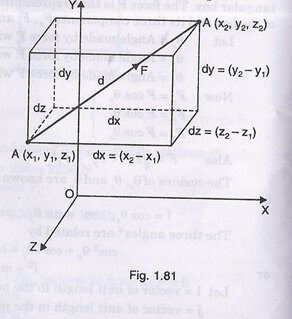
Suppose two points A (x₁, y₁, z₁) and A (x₂, y₂, z₂) are given on the line of action of applied force as shown in Fig. 1.81,

d be the distance between the points

dx be distance between the points inxy plane

dy be distance between the points in yz plane

dzbe distance between the points in zx plane

θx be angle with x-axis

θy be angle with y-axis

θz be angle with z-axis

Then,

Magnitude of distance between the points in different planes can be given by-

dx = (x2 – x1) = d cosθx

dy = (y2 – y1) = d cosθy

dz = (z2 – z1) = d cosθz

Determine the Position Vector

Consider two similar points B (x₁, y₁, z₁) and A (x₂, y₂, z₂) at a distance of d as shown in Fig. 1.82-

To find the position vector, we consider the origin w.r.t. another point.

So, position vector of point A w.r.t. point O can be given by-

r = xi ̂+ yj ̂+ jk ̂

And,

Position vector of point A w.r.t. point B can be given by-

r = (x2 – x1)  i ̂+ (y2 – y1)  j ̂+ (z2 – z1)  k ̂

Links of Previous Main Topic:-

• Fluid statics introduction
• Manometers measurement pressure
• Fluid kinematics
• Bernoullis equation
• Basics and statics of particles introduction
• Units and dimensions
• Laws of mechanics in basics and statics of particles
• Lamis theorem in basics and statics of particles
• Parallelogram and triangular law of forces
• Vectors
• Resolution and composition of a force
• Coplanar forces
• Resultant of coplanar forces
• Equilibrium of a particle
• Equilibrium of a rigid body
• Forces in space

Links of Next Mechanical Engineering Topics:-

• Resultant of coplanar forces
• Equilibrium of a particle
• Equilibrium of a rigid body
• Forces in space
• Equilibrium of a particle in space
• Equivalent system of forces
• Principle of transmissibility
• Single equivalent force
• Highlights of basics and statics of particles
• Equilibrium of rigid bodies introduction