When the force system gets its resultant along the line of action of force in the same plane, it is called equilibrant. Similar arbitrary point can also be shown for moment of forces about the point of resultant of force. Thus, it is called the equivalent system of forces that can be formed because of two reasons-
- System of concurrent forces
Let us consider three forces F1, F2 and F3act on a rigid body in different direction such that force F1 and F2 have different directions than force F3.
Then,
Resultant force can be given by-
R = F1 + F2+ F3 + …… (In the direction of force F3)
- System of couples
Similarly, if the moment of forces F1, F2 and F3 are considered such that resultant of moment of force give the direction about point of resultant of force, then it can be given by-
M = M1 + M2 + M3 + ……..
Problems on Equivalent Systems of Forces
Example:
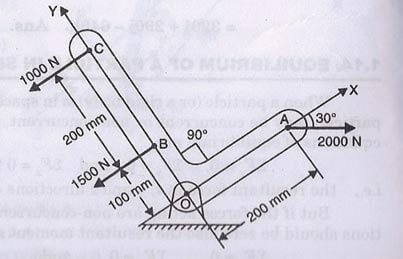
Fig. 1.87 shows L-shaped body. Find the magnitude of three external forces which are acting on it such that the body will have equivalent system through point O.
Solution:
Given Data:
Force at A, F1 = 2000 N
Force at B, F2 = 1500 N
Force at C, F3 = 1000 N
OA = 200 mm
OB = 100 mm
BC = 200 mm
Force, F1 making an angle 300with the X-axis as shown in above figure
We consider,
Resultant R will be passing through a point and moment MR
Now,
Components ofF1 can be given by-
Along x-axis, F1x = 2000 x cos 300= 1732 N
Along y-axis, F1y = 2000 x sin 300= 1000 N
According to the equilibrium of forces, we can write-
∑▒〖F_x=〗1732 – 1500 – 1000
= – 768 N
∑▒〖F_y=〗 – 1000N
Resultant can be given by-
R = √(∑▒F_x 2+ ∑▒F_y 2)
= √[(– 768)2+ (– 1000)2]
R = 1260.88 N
Now,
Moment of forces at point O can be given by-
M = – 1000 x 200 + 1500 x 100 + 1000 x 300
= 250000 Nmm
Or,
M = 250 Nm
Links of Previous Main Topic:-
- Fluid statics introduction
- Manometers measurement pressure
- Fluid kinematics
- Bernoullis equation
- Basics and statics of particles introduction
- Units and dimensions
- Laws of mechanics in basics and statics of particles
- Lamis theorem in basics and statics of particles
- Parallelogram and triangular law of forces
- Vectors
- Resolution and composition of a force
- Coplanar forces
- Resultant of coplanar forces
- Equilibrium of a particle
- Equilibrium of a rigid body
- Forces in space
Links of Next Mechanical Engineering Topics:-