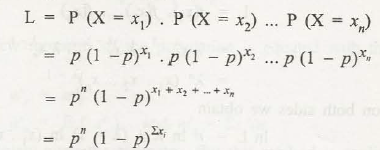Point estimation is the process of estimation where sampling is used when single value is estimated for the unknown parameter of a population. There are two methods of point estimation which are used. They are:
- Method of maximum likelihood
Properties of maximum likelihood
- It is consistent, most efficient and sufficient with the provision that there exists a sufficient estimator.
- It is not unbiased.
- It is generally distributed normally for large samples.
- If g(is a function of and e is the maximum likelihood of it, then g(is an maximum likelihood of g(
Let x₁, x₂, …,be a random sample from a population whose pmf (discrete case) or pdf (continuous case ) is f (x, θ) where θ is the parameter. Then construct the likelihood function as follows:
L = f (x₁, θ) .f (x₂, θ) … f (, θ)
Since log L is maximum when L is maximum, therefore to obtain the estimate of θ, we maximize L as follows,
And is known as MLE or maximum likelihood estimator.
Example 1:
A discrete random variable X can take up all non-negative integers and P (X= r) = p (1- p)r (r = 0, 1, 2, .. .)Here, p (0 <p <I) is the parameter of the distribution. Find the MLE of p for a sample of size: x₁, x₂, …, from the population of X.
Solution:
Consider the following: L= P(X= x₁). P(X= x₂)… P(X= )
= p
=
=
Taking log on both sides,
= 0
=
=
at
=
Hence the MLE of p is 1/ 1+x
Example 2:
A random variable X has a distribution with density function: f (x) = λ x λ -1(0 < x < 1) where A is the parameter. Find the MLE of A for a sample of size n. x₁, x₂, …,, from the population of X.
Solution:
Consider the following
L= (x₁).f (x₂)….f ()
= λ x₁ λ -1 .λ x₂ λ -1 ….λ
=
Taking log on both sides,
ln L = n ln A. + (A.- 1) ln (x1,x2,…, )
Also,
Hence, MLE of A is
Example 3:
X tossed a biased coin 40 times and got head 15 times, while Y tossed it 50 times and got head 30 times. Find the MLE of the probability of getting head when the coin is tossed.
Solution:
Let P be the unknown probability of getting a head.
Using binomial distribution, Probability of getting 15 heads in 40 tosses
Probability of getting 30 heads in 50 tosses
The likelihood function is taken by multiplying these probabilities.
L=
Log L = log [ + 45log (1-p)
which is the MLE.
- Method of moments
In this particular method, the first few moments of a population is equated with the equivalent moments of the same sample.
Then, µ’r = m’r
Where ) and
The method is only applicable when the population moment exists and the solution for the parameters gives the estimates.
Example:
Estimate the parameter p of the binomial distribution by the method of moments when n is known.
Solution:
np=
p= and that is the value estimated.
Links of Previous Main Topic:-
- Introduction to statistics
- Knowledge of central tendency or location
- Definition of dispersion
- Moments
- Bivariate distribution
- Theorem of total probability addition theorem
- Random variable
- Binomial distribution
- What is sampling
- Estimation
Links of Next Statistics Topics:-
- Statistical hypothesis and related terms
- Analysis of variance introduction
- Definition of stochastic process
- Introduction operations research
- Introduction and mathematical formulation in transportation problems
- Introduction and mathematical formulation
- Queuing theory introduction
- Inventory control introduction
- Simulation introduction
- Time calculations in network
- Introduction of game theory