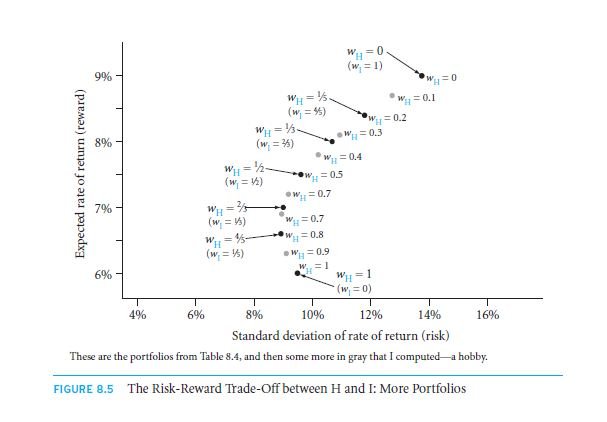
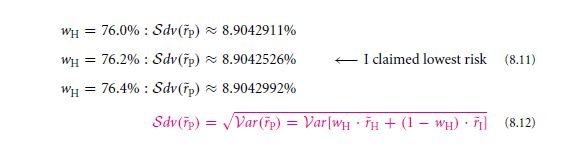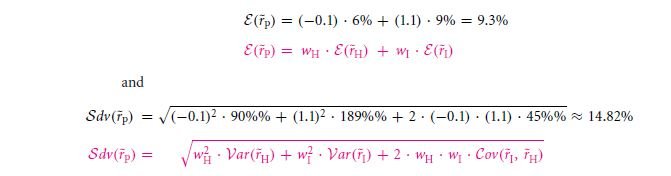We shall now plot graphs for our analysis. The x axis would have the portfolio risks against the y axis that contains the portfolio rewards. This graph has been plotted with reference to the table named 8.4 present on page numbered as 232. Few more portfolios were added to make us understand the graph better. Before using it the risk supplemented with reward value of the added portfolio is calculated and entered on to the table. We must now notice the pattern in the graph.
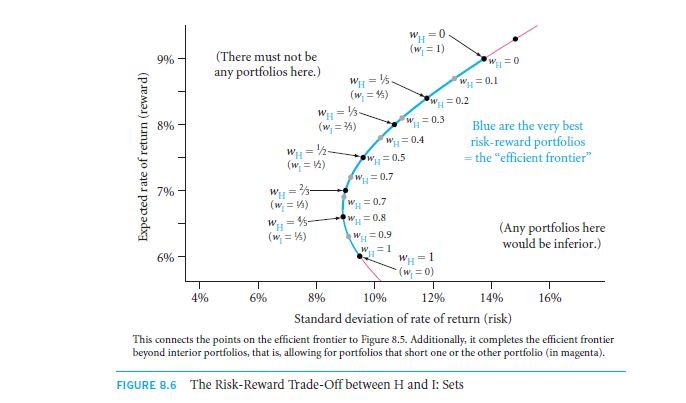
Say if we choose some extra portfolios along with the range of investments that weighs on H within the range 0 to 100%, then subsequently we might conclude with what we get in fig: 8.6. Mean Variance Efficient frontier (abbreviated as MVE frontier) is what the curve obtained is named. The area under the curve gives the finest risk as well as reward portfolio. Ideally there wouldn’t be any portfolio to the North West part of this region.
Those portfolios would be having a greater amount of profit for a certain specified risk, and also lesser risk meant for a known probable degree of yield. In case if such region of portfolios existed then this would have eventually be called the MVE frontier. Taking standard deviation on the x axis, we obtain a hyperbola (the name of the nature of the curve).
Allowing Shorted Positions
The portfolio on the extreme left of the efficient region is termed as minimum variance range of investments. It is so called as from here a collection of funds with a reduced risk cannot be obtained.
It involves considerable amount of algebra so as to find out the risk rate. With reference to the example we considered, the portfolio with a weight valued at 76.191% upon H and also 23.809% upon I. Post the calculation we see that it gets a low risk as low as 8.9%.
Links of Previous Main Topic:-
- Investor choice risk and reward
- Portfolios diversification and investor preferences
- How to measure risk contribution
- Expected rates of return and market betas for weighted portfolios and firms
- Spreadsheet calculations for risk and reward
- An investors specific trade off between risk and reward
- A shortcut formula for the risk of a portfolio
Links of Previous Main Topic:-
- Adding a risk free asset
- Equity payouts
- For value financial structure and corporate strategy analysis
- Capital structure dynamics firm scale
- Capital structure patterns in the united states
- Investment banking and mergers and acquisitions
- Corporate governance
- International finance
- Options and risk management